统计
本用户指南部分介绍了数学表达式中可用的核心统计函数。
描述性统计
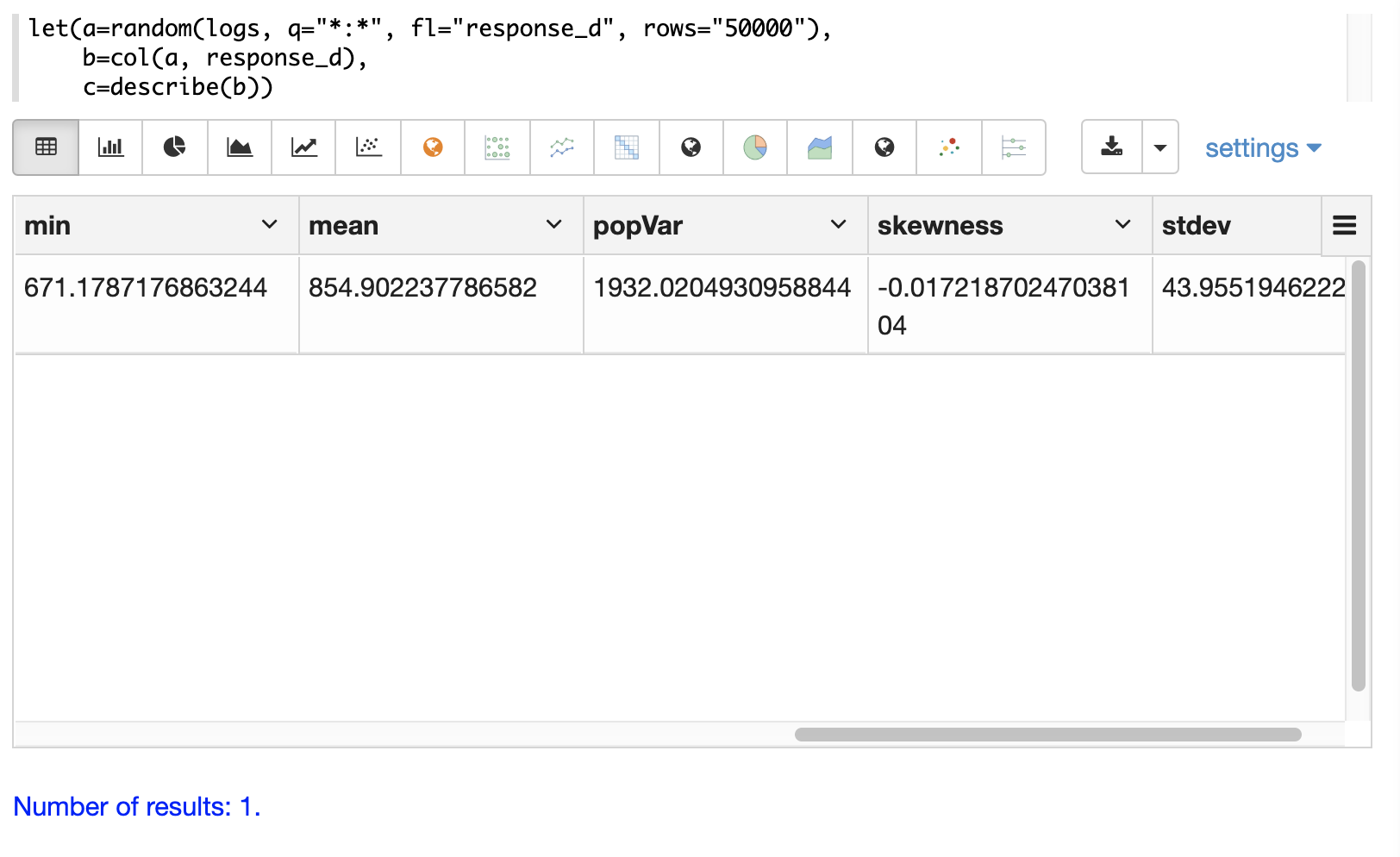
describe 函数返回数值数组的描述性统计信息。describe 函数返回一个包含描述性统计信息的名称/值对的单个元组。
以下是一个简单示例,它从 logs 集合中选择一个随机文档样本,将结果集中的 response_d 字段向量化,并使用 describe 函数返回有关该向量的描述性统计信息。
let(a=random(logs, q="*:*", fl="response_d", rows="50000"),
b=col(a, response_d),
c=describe(b))当此表达式发送到 /stream 处理程序时,它会响应
{
"result-set": {
"docs": [
{
"sumsq": 36674200601.78738,
"max": 1068.854686837548,
"var": 1957.9752647562789,
"geometricMean": 854.1445499569674,
"sum": 42764648.83319176,
"kurtosis": 0.013189848821424377,
"N": 50000,
"min": 656.023249311864,
"mean": 855.2929766638425,
"popVar": 1957.936105250984,
"skewness": 0.0014560741802307174,
"stdev": 44.24901428005237
},
{
"EOF": true,
"RESPONSE_TIME": 430
}
]
}
}请注意,随机样本包含 50,000 条记录,响应时间仅为 430 毫秒。此大小的样本可用于可靠地估计非常大的基础数据集的统计信息,并且具有亚秒级的性能。
describe 函数也可以使用 Zeppelin-Solr 在表格中可视化
直方图和频率表
直方图和频率表是可视化随机变量分布的工具。
hist 函数创建用于连续数据的直方图。freqTable 函数创建用于离散数据的频率表。
直方图
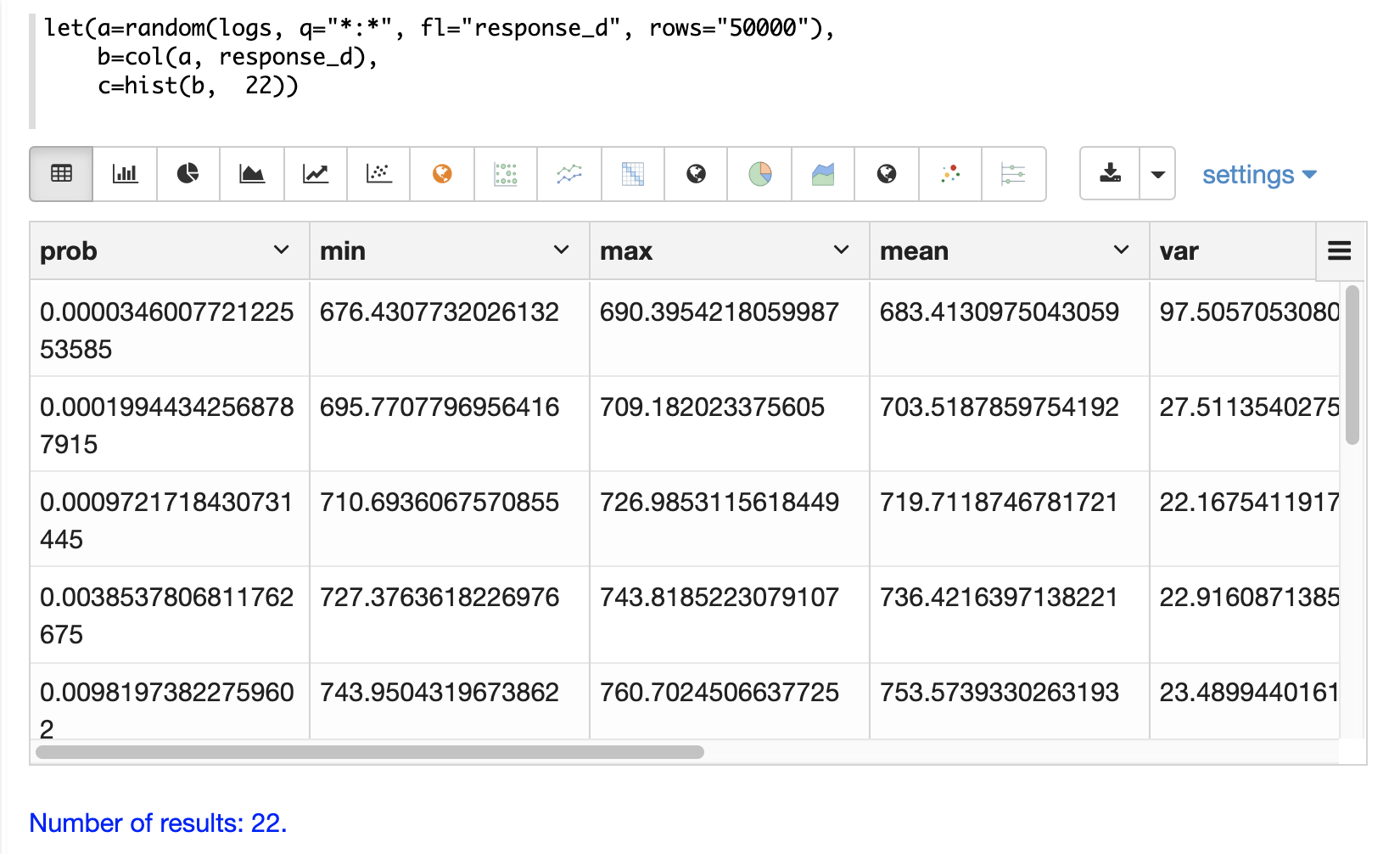
在下面的示例中,使用直方图来可视化 logs 集合中响应时间的随机样本。该示例使用 random 函数检索随机样本,并从结果集中的 response_d 字段创建向量。然后,将 hist 函数应用于该向量,以返回包含 22 个 bin 的直方图。hist 函数返回一个元组列表,其中包含每个 bin 的摘要统计信息。
let(a=random(logs, q="*:*", fl="response_d", rows="50000"),
b=col(a, response_d),
c=hist(b, 22))当此表达式发送到 /stream 处理程序时,它会响应
{
"result-set": {
"docs": [
{
"prob": 0.00004896007228311655,
"min": 675.573084576817,
"max": 688.3309631697003,
"mean": 683.805542728906,
"var": 50.9974629924082,
"cumProb": 0.000030022417162809913,
"sum": 2051.416628186718,
"stdev": 7.141250800273591,
"N": 3
},
{
"prob": 0.00029607514624062624,
"min": 696.2875238591652,
"max": 707.9706315779541,
"mean": 702.1110569558929,
"var": 14.136444379466969,
"cumProb": 0.00022705264963879807,
"sum": 11233.776911294284,
"stdev": 3.759846323916307,
"N": 16
},
{
"prob": 0.0011491235433157194,
"min": 709.1574910598678,
"max": 724.9027194369135,
"mean": 717.8554290699951,
"var": 20.6935845290122,
"cumProb": 0.0009858515418689757,
"sum": 41635.61488605971,
"stdev": 4.549020172412098,
"N": 58
},
...
]}}使用 Zeppelin-Solr,直方图可以首先可视化为表格
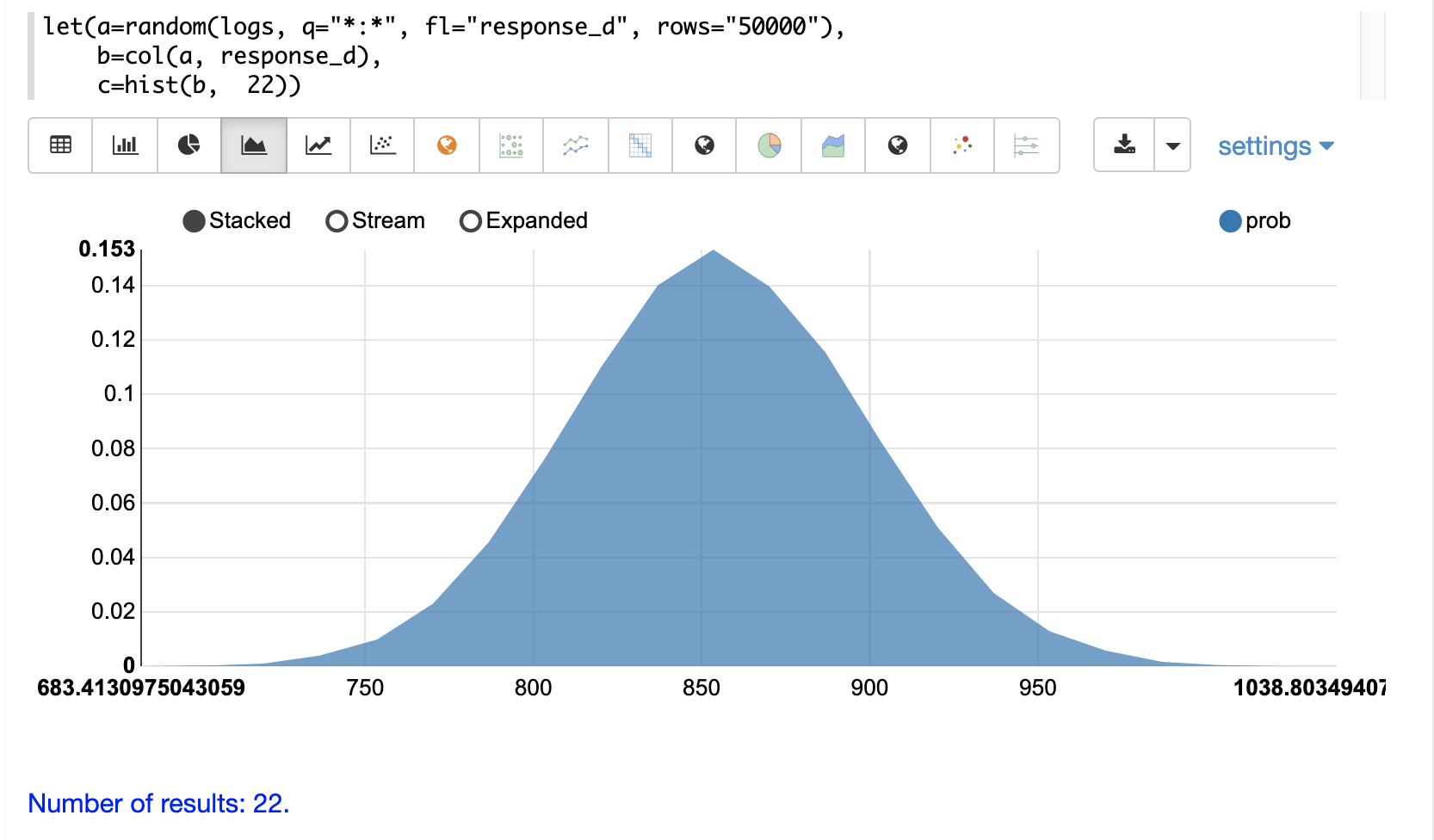
然后,可以通过在 x 轴上绘制 bin 的均值,在 y 轴上绘制 prob(概率)来使用面积图可视化直方图
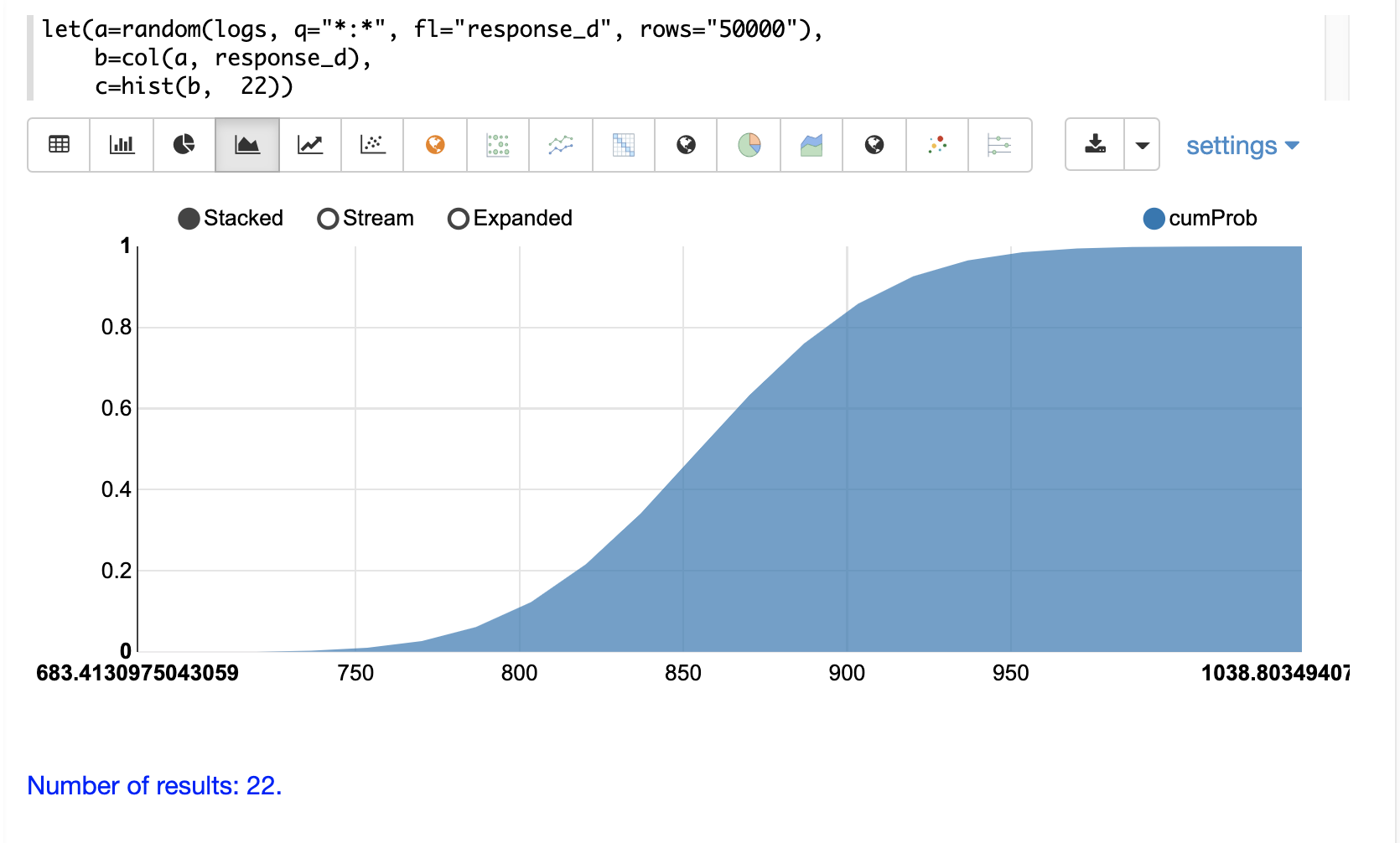
可以通过将 y 轴切换到 cumProb 列来绘制累积概率
自定义直方图
可以通过将多个 stats 函数的输出组合到单个直方图中来定义和可视化自定义直方图。自定义直方图不是自动对数值字段进行分箱,而是允许基于查询比较 bin。
用户指南的搜索、采样和聚合部分首先讨论了 stats 函数。 |
一个简单的示例将说明如何定义和可视化自定义直方图。
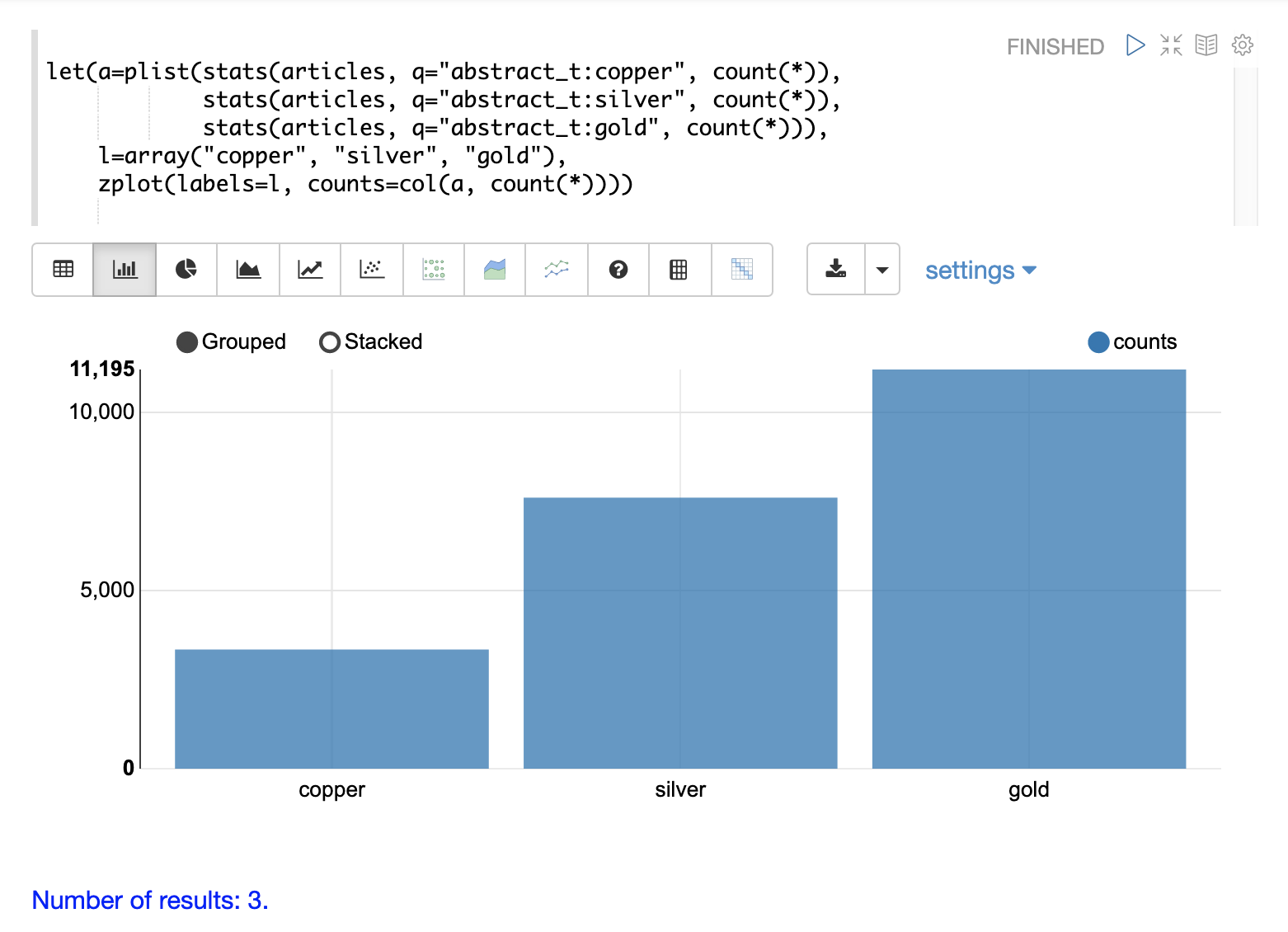
在此示例中,三个 stats 函数被包装在一个 plist 函数中。plist(并行列表)函数并行执行其每个内部函数,并将结果连接到单个流中。plist 还维护每个子函数输出的顺序。在此示例中,每个 stats 函数都计算与特定查询匹配的文档数。在这种情况下,它们会计算包含术语 copper、gold 和 silver 的文档数。包含计数的元组列表然后存储在变量 a 中。
然后,创建一个标签的 array 并将其设置为变量 l。
最后,使用 zplot 函数绘制标签向量和 count(*) 列。请注意,col 函数在 zplot 函数内部使用,以从 stats 结果中提取计数。
频率表
freqTable 函数返回离散数据集的频率分布。freqTable 函数不像直方图那样创建 bin。相反,它计算每个离散数据值的出现次数,并返回一个元组列表,其中包含每个值的频率统计信息。
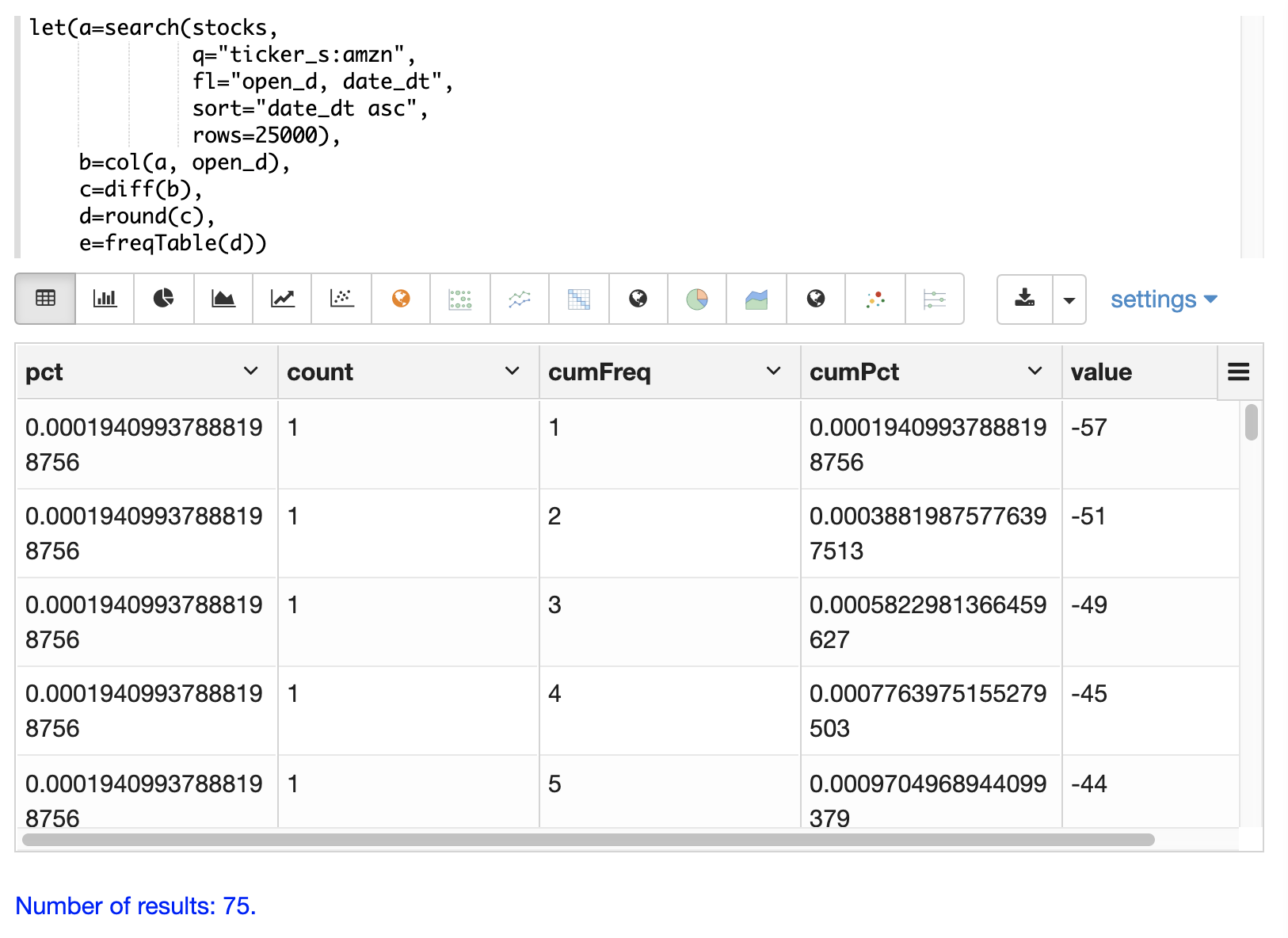
以下是一个频率表的示例,该表是从股票代码 amzn 的每日开盘股票价格的四舍五入的差额的结果集中构建的。
这个例子很有趣,因为它展示了一个多步骤的过程来获得结果。第一步是在 stocks 集合中 搜索 股票代码为 amzn 的记录。请注意,结果集按日期升序排序,并返回 open_d 字段,该字段是当天的开盘价。
然后,将 open_d 字段向量化并设置为变量 b,现在该变量包含按日期升序排列的开盘价向量。
然后使用 diff 函数来计算开盘价向量的 一阶差分。一阶差分只是从数组中的每个值中减去前一个值。这将提供一个每日价格差异的数组,该数组将显示每日开盘价的变化。
然后,使用 round 函数将价格差异四舍五入到最接近的整数,以创建离散值的向量。在此示例中,round 函数有效地在整数边界处对连续数据进行 分箱。
最后,在离散值上运行 freqTable 函数以计算频率表。
let(a=search(stocks,
q="ticker_s:amzn",
fl="open_d, date_dt",
sort="date_dt asc",
rows=25000),
b=col(a, open_d),
c=diff(b),
d=round(c),
e=freqTable(d))当此表达式发送到 /stream 处理程序时,它会响应
{
"result-set": {
"docs": [
{
"pct": 0.00019409937888198756,
"count": 1,
"cumFreq": 1,
"cumPct": 0.00019409937888198756,
"value": -57
},
{
"pct": 0.00019409937888198756,
"count": 1,
"cumFreq": 2,
"cumPct": 0.00038819875776397513,
"value": -51
},
{
"pct": 0.00019409937888198756,
"count": 1,
"cumFreq": 3,
"cumPct": 0.0005822981366459627,
"value": -49
},
...
]}}使用 Zeppelin-Solr,频率表可以首先可视化为表格
然后,可以通过切换到散点图并选择 value 列作为 x 轴,选择 count 列作为 y 轴来绘制频率表
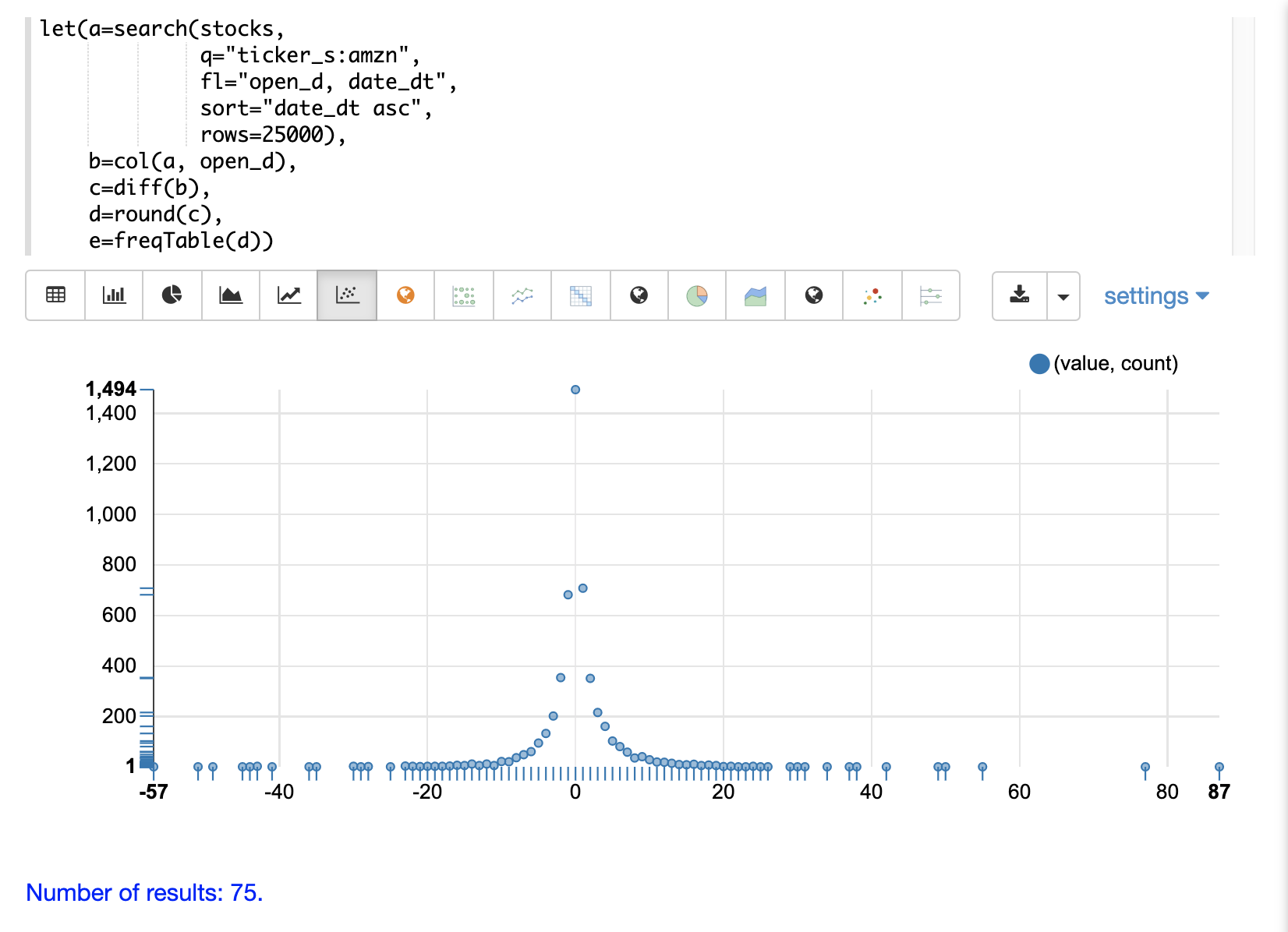
请注意,可视化清晰地显示了股票价格每日变化的频率(四舍五入到整数)。最频繁出现的值是 0,出现 1494 次,其次是 -1 和 1,出现约 700 次。
百分位数
percentile 函数返回样本集中特定百分位数的估计值。下面的示例返回一个随机样本,其中包含 logs 集合中的 response_d 字段。response_d 字段被向量化,并计算该向量的第 20 个百分位数。
let(a=random(logs, q="*:*", rows="15000", fl="response_d"),
b=col(a, response_d),
c=percentile(b, 20))当此表达式发送到 /stream 处理程序时,它会响应
{
"result-set": {
"docs": [
{
"c": 818.073554
},
{
"EOF": true,
"RESPONSE_TIME": 286
}
]
}
}percentile 函数还可以计算百分位数的值数组。下面的示例计算 response_d 字段的随机样本的第 20、40、60 和 80 个百分位数。
let(a=random(logs, q="*:*", rows="15000", fl="response_d"),
b=col(a, response_d),
c=percentile(b, array(20,40,60,80)))当此表达式发送到 /stream 处理程序时,它会响应
{
"result-set": {
"docs": [
{
"c": [
818.0835543394625,
843.5590348165282,
866.1789509894824,
892.5033386599067
]
},
{
"EOF": true,
"RESPONSE_TIME": 291
}
]
}
}分位数图
分位数图或 QQ 图是用于直观比较两个或多个分布的强大工具。
分位数图在同一可视化中绘制两个或多个分布的百分位数。这允许在每个百分位数对分布进行可视化比较。一个简单的例子将有助于说明分位数图的强大功能。
在此示例中,使用分位数图可视化了两个股票代码 goog 和 amzn 的每日股票价格变化分布。
该示例首先创建一个表示将要计算的百分位数的数组,并将此数组设置为变量 p。然后,为股票代码 amzn 和 goog 抽取 change_d 字段的随机样本。change_d 字段表示一天内的股票价格变化。然后,将 change_d 字段向量化为两个样本,并放置在变量 amzn 和 goog 中。然后,使用 percentile 函数计算两个向量的百分位数。请注意,变量 p 用于指定计算的百分位数列表。
最后,使用 zplot 在 x 轴 上绘制百分位数序列,在 y 轴 上绘制两个分布的计算出的百分位数。并使用折线图来可视化 QQ 图。
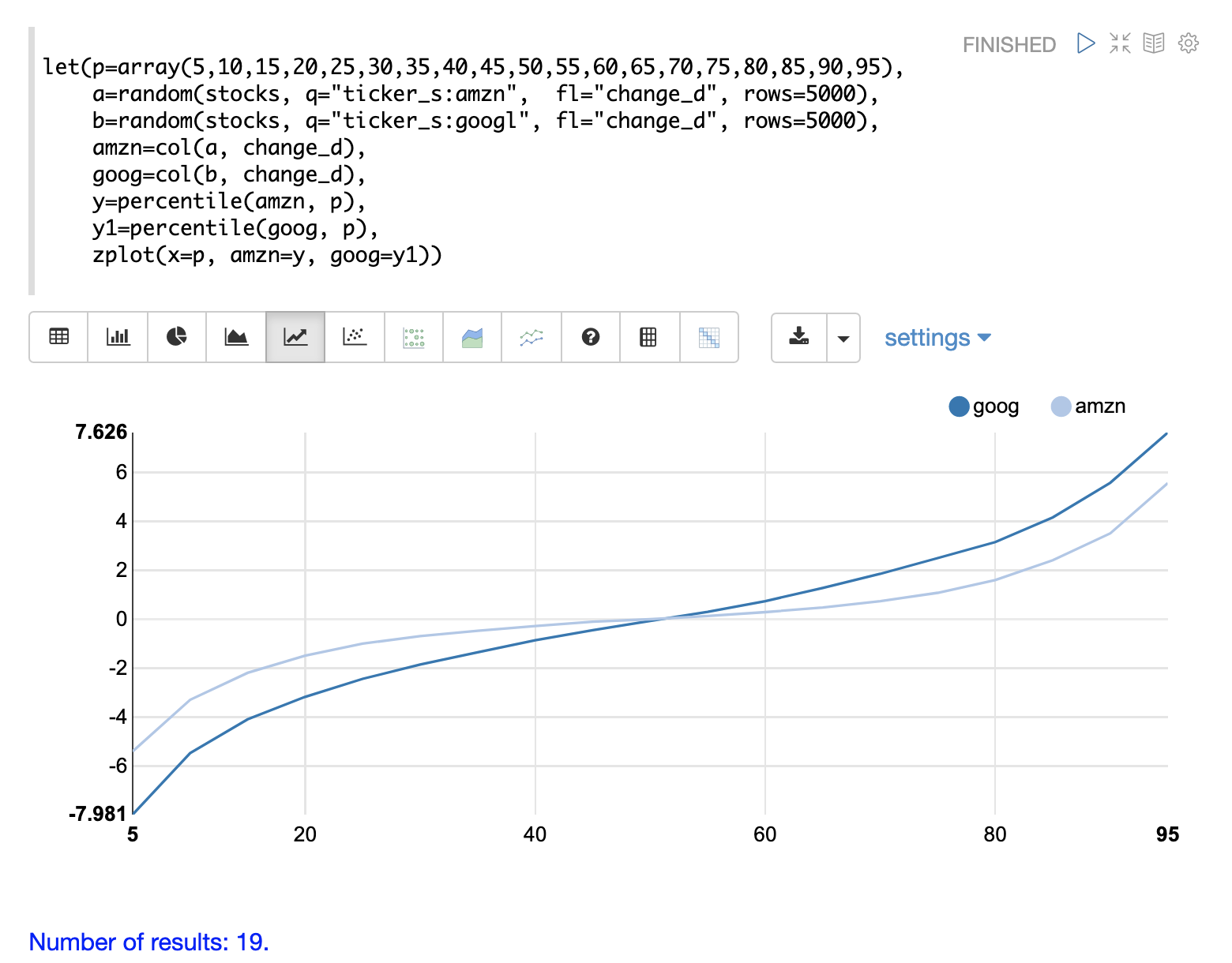
此分位数图提供了 amzn 和 googl 每日价格变化分布的清晰视图。在图中,x 轴 是百分位数,而 y 轴 是计算出的百分位数值。
请注意,goog 百分位数值的起始值较低,最终值高于 amzn 图,并且斜率更陡峭。这表明 goog 价格变化分布的变异性更大。该图清晰地显示了整个百分位数范围内分布的差异。
相关性和协方差
相关性和协方差衡量随机变量如何一起波动。
相关性和相关矩阵
相关性是衡量两个向量之间线性相关性的指标。相关性的范围在 -1 到 1 之间。
支持三种相关类型
-
pearsons(默认)
-
kendalls
-
spearmans
通过在函数调用中添加 type 命名参数来指定相关性类型。
在下面的示例中,使用 random 函数从 logs 集合中抽取一个包含两个字段 filesize_d 和 response_d 的随机样本。这些字段被向量化到变量 x 和 y 中,然后使用 corr 函数计算两个向量的 Spearman's 相关性。
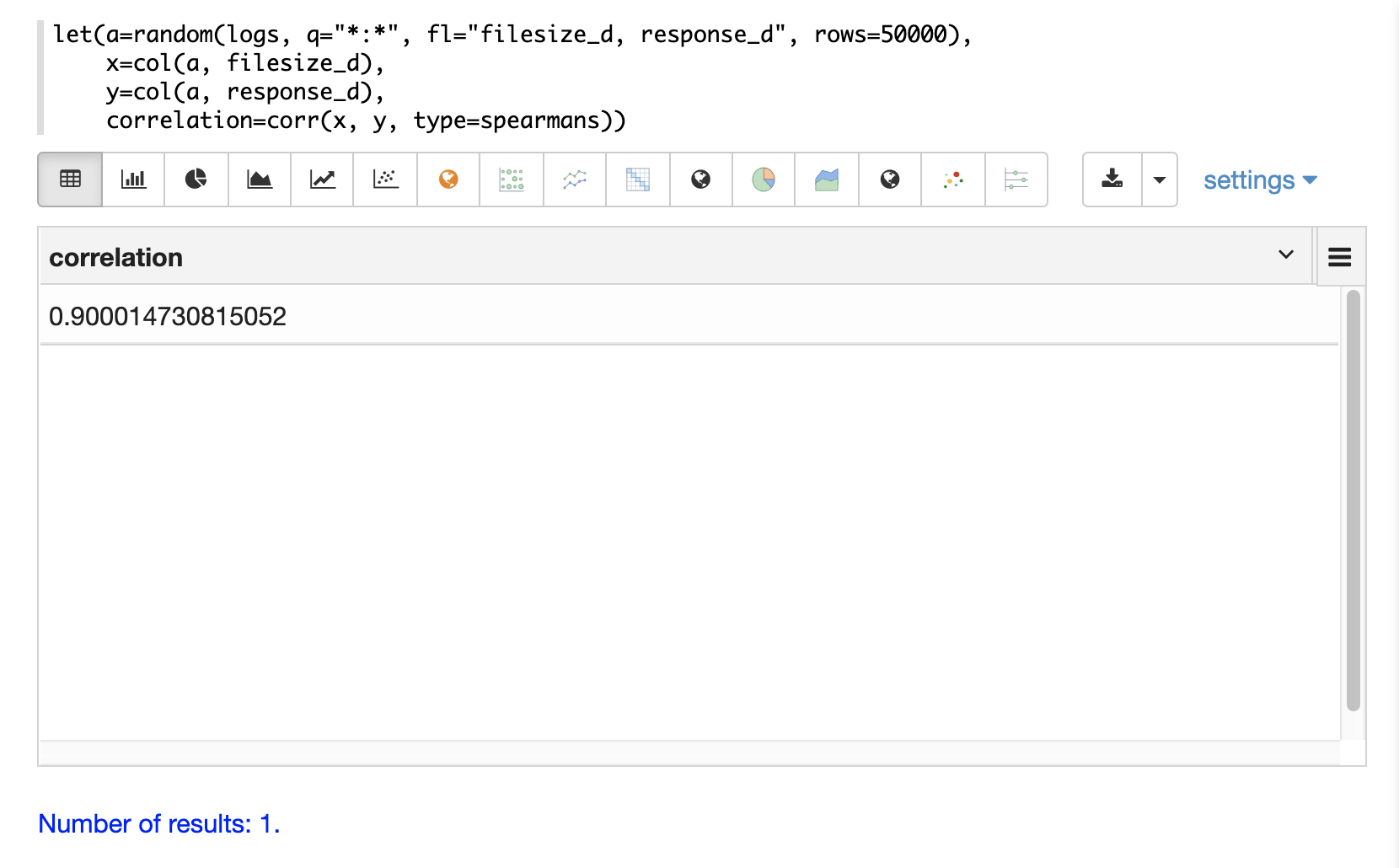
相关矩阵
相关矩阵是可视化两个或多个向量之间相关性的强大工具。
如果将矩阵作为参数传递,则 corr 函数会构建相关矩阵。相关矩阵是通过关联矩阵的 列 来计算的。
下面的示例演示了相关矩阵与二维分面结合的强大功能。
在此示例中,使用 facet2D 函数在 nyc311 投诉数据库中的 complaint_type_s 和 zip_s 字段上生成二维分面聚合。聚合了 前 20 个 投诉类型和每个投诉类型的 前 25 个 邮政编码。结果是包含字段 complaint_type_s、zip_s 和该对的计数的元组流。
然后使用 pivot 函数将字段透视为 矩阵,其中 zip_s 字段作为 行,complaint_type_s 字段作为 列。count(*) 字段填充矩阵单元格中的值。
然后使用 corr 函数关联矩阵的 列。这将生成一个相关矩阵,该矩阵显示投诉类型如何基于它们出现的邮政编码相关。看待此问题的另一种方式是,它显示了不同投诉类型在邮政编码中共同出现的趋势。
最后,使用 zplot 函数将相关矩阵绘制为热图。
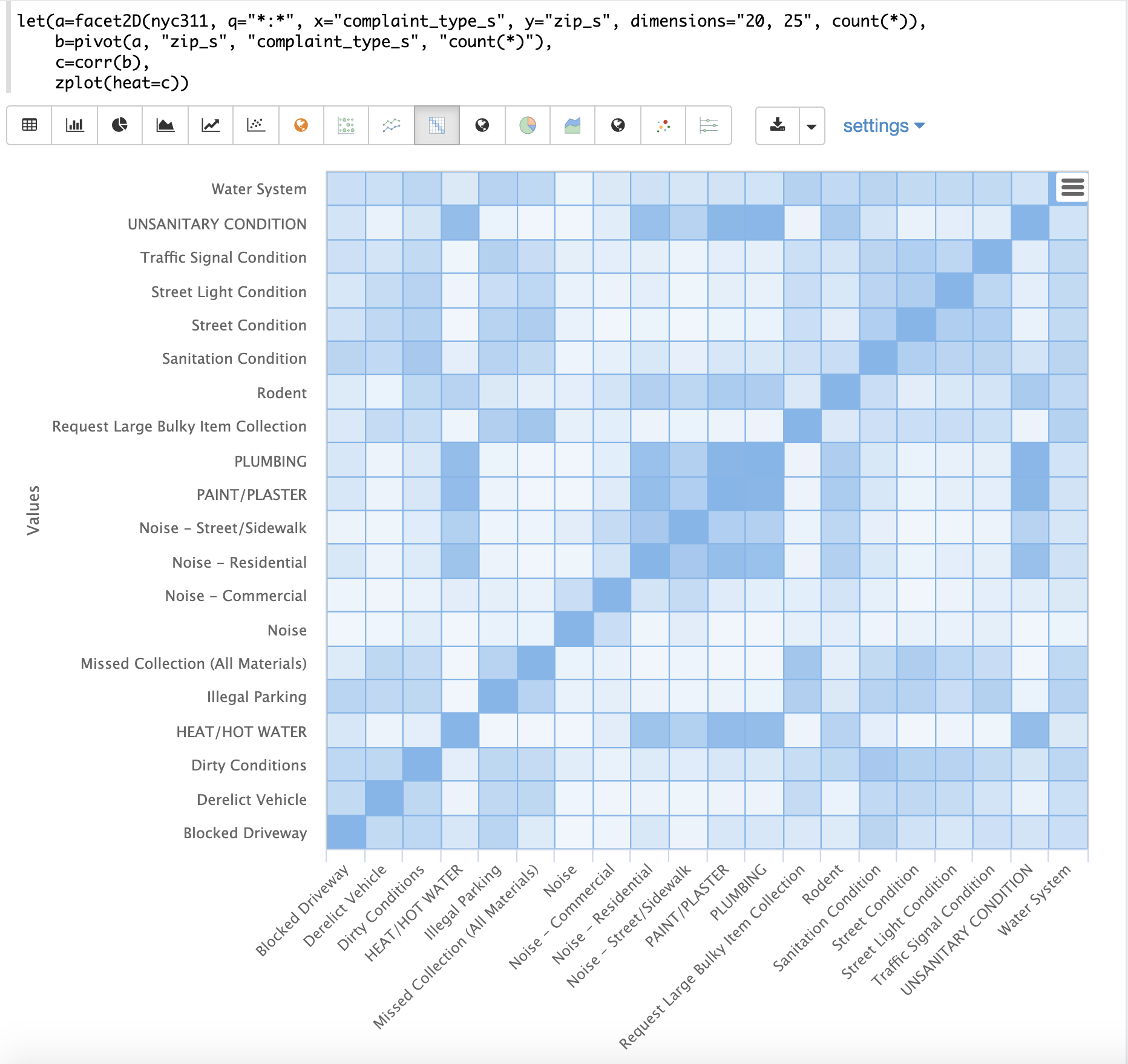
请注意,在该示例中,相关矩阵是方形的,投诉类型显示在 x 轴和 y 轴上。热图中单元格的颜色显示了投诉类型之间相关性的强度。
热图是交互式的,因此将鼠标悬停在其中一个单元格上会弹出该单元格的值。
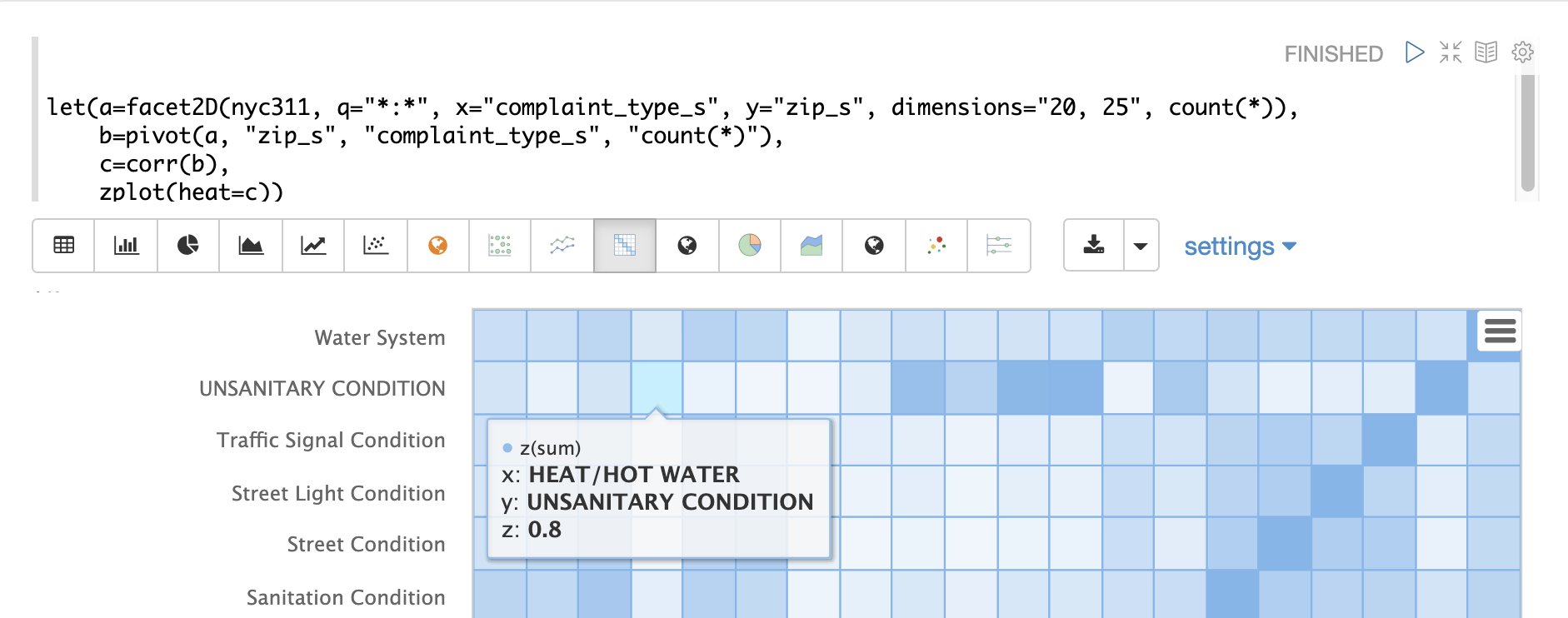
请注意,HEAT/HOT WATER 和 UNSANITARY CONDITION 投诉的相关性为 8(四舍五入到最接近的十分位)。
协方差和协方差矩阵
协方差是相关性的未缩放度量。
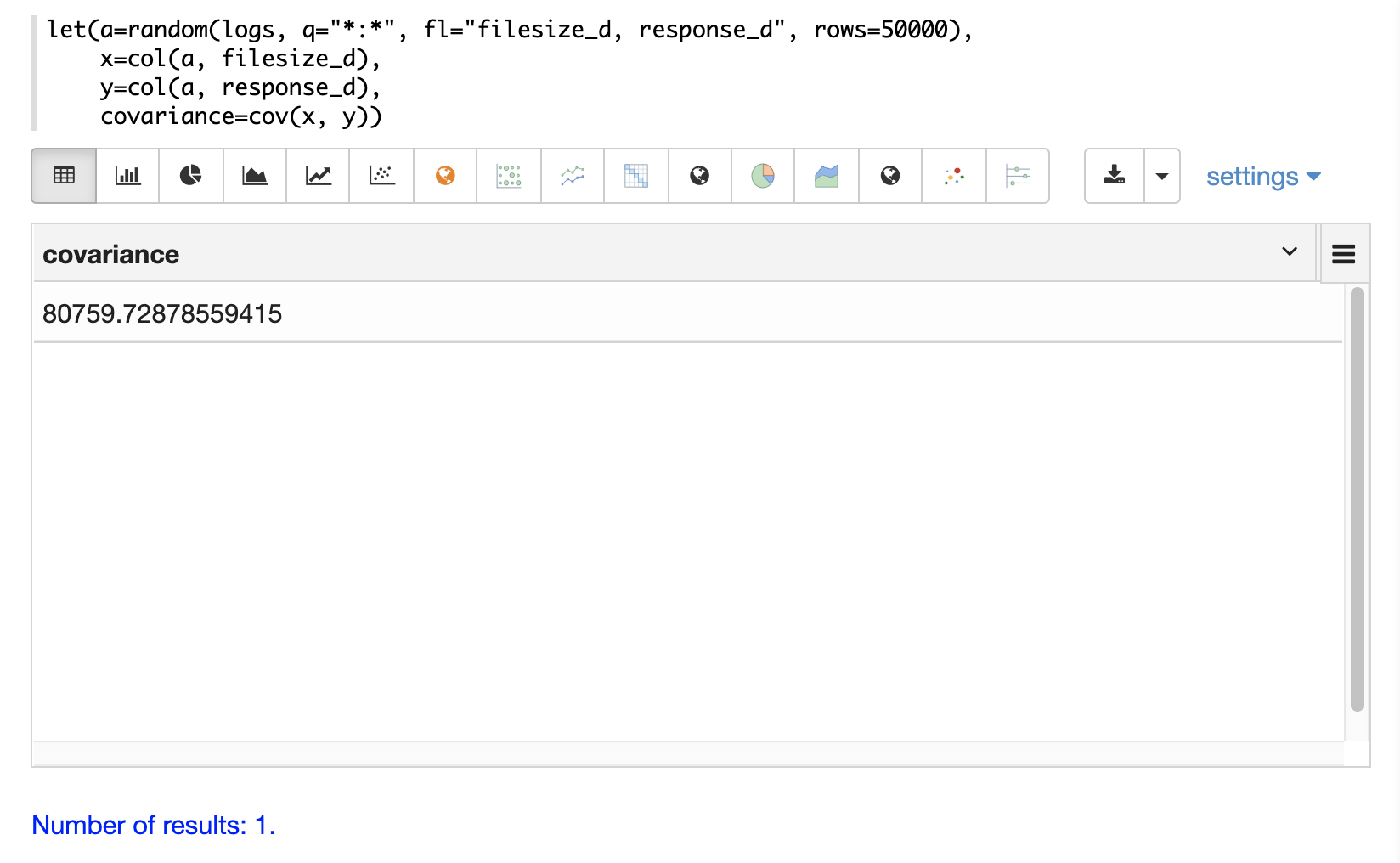
cov 函数计算两个数据向量的协方差。
在下面的示例中,使用 random 函数从 logs 集合中抽取一个包含两个字段 filesize_d 和 response_d 的随机样本。这些字段被向量化到变量 x 和 y 中,然后使用 cov 函数计算两个向量的协方差。
如果将矩阵传递给 cov 函数,它将自动计算矩阵 列 的协方差矩阵。
请注意,在下面的示例中,x 和 y 向量被添加到矩阵中。然后转置该矩阵以将行转换为列,并为矩阵的列计算协方差矩阵。
let(a=random(logs, q="*:*", fl="filesize_d, response_d", rows=50000),
x=col(a, filesize_d),
y=col(a, response_d),
m=transpose(matrix(x, y)),
covariance=cov(m))当此表达式发送到 /stream 处理程序时,它会响应
{
"result-set": {
"docs": [
{
"covariance": [
[
4018404.072532102,
80243.3948172242
],
[
80243.3948172242,
1948.3216661122592
]
]
},
{
"EOF": true,
"RESPONSE_TIME": 534
}
]
}
}协方差矩阵包含两个向量的方差和向量之间的协方差,格式如下
x y
x [4018404.072532102, 80243.3948172242],
y [80243.3948172242, 1948.3216661122592]协方差矩阵始终是方形的。因此,由 3 个向量创建的协方差矩阵将生成一个 3 x 3 矩阵。
统计推断检验
统计推断检验在 随机样本 上检验假设,并返回 p 值,该 p 值可用于推断整个总体的检验可靠性。
以下统计推断检验可用
-
anova:单向方差分析检验两个或多个随机样本的均值是否存在统计上的显着差异。 -
ttest:T 检验检验两个随机样本的均值是否存在统计上的显着差异。 -
pairedTtest:配对 t 检验检验具有配对数据的两个随机样本的均值是否存在统计上的显着差异。 -
gTestDataSet:G 检验检验两个离散分箱数据的样本是否是从同一总体中抽取的。 -
chiSquareDataset:卡方检验检验两个离散分箱数据的样本是否是从同一总体中抽取的。 -
mannWhitney:Mann-Whitney 检验是一种非参数检验,用于检验两个连续数据的样本是否是从同一总体中抽取的。当不满足 T 检验的潜在假设时,通常使用 Mann-Whitney 检验代替 T 检验。 -
ks:Kolmogorov-Smirnov 检验检验两个连续数据的样本是否是从同一分布中抽取的。
下面是在两个随机样本上执行 T 检验的简单示例。返回的 p 值为 0.93,这意味着我们可以接受原假设,即两个样本的均值没有统计上的显着差异。
let(a=random(collection1, q="*:*", rows="1500", fl="price_f"),
b=random(collection1, q="*:*", rows="1500", fl="price_f"),
c=col(a, price_f),
d=col(b, price_f),
e=ttest(c, d))当此表达式发送到 /stream 处理程序时,它会响应
{
"result-set": {
"docs": [
{
"e": {
"p-value": 0.9350135639249795,
"t-statistic": 0.081545541074817
}
},
{
"EOF": true,
"RESPONSE_TIME": 48
}
]
}
}转换
在统计分析中,在执行统计计算之前转换数据集通常很有用。统计函数库包括以下常用的转换
-
rank:返回一个数值数组,其中包含原始数组中每个元素的排名转换值。 -
log:返回一个数值数组,其中包含原始数组中每个元素的自然对数。 -
log10:返回一个数值数组,其中包含原始数组中每个元素的以 10 为底的对数。 -
sqrt:返回一个数值数组,其中包含原始数组中每个元素的平方根。 -
cbrt:返回一个数值数组,其中包含原始数组中每个元素的立方根。 -
recip:返回一个数值数组,其中包含原始数组中每个元素的倒数。
下面是一个对数转换数据集执行 t 检验的示例
let(a=random(collection1, q="*:*", rows="1500", fl="price_f"),
b=random(collection1, q="*:*", rows="1500", fl="price_f"),
c=log(col(a, price_f)),
d=log(col(b, price_f)),
e=ttest(c, d))当此表达式发送到 /stream 处理程序时,它会响应
{
"result-set": {
"docs": [
{
"e": {
"p-value": 0.9655110070265056,
"t-statistic": -0.04324265449471238
}
},
{
"EOF": true,
"RESPONSE_TIME": 58
}
]
}
}反向转换
使用 log、log10、sqrt 和 cbrt 函数转换的向量可以使用 pow 函数进行反向转换。
下面的示例展示了如何反向转换由 sqrt 函数转换的数据。
let(echo="b,c",
a=array(100, 200, 300),
b=sqrt(a),
c=pow(b, 2))当此表达式发送到 /stream 处理程序时,它会响应
{
"result-set": {
"docs": [
{
"b": [
10,
14.142135623730951,
17.320508075688775
],
"c": [
100,
200.00000000000003,
300.00000000000006
]
},
{
"EOF": true,
"RESPONSE_TIME": 0
}
]
}
}下面的示例展示了如何反向转换由 log10 函数转换的数据。
let(echo="b,c",
a=array(100, 200, 300),
b=log10(a),
c=pow(10, b))当此表达式发送到 /stream 处理程序时,它会响应
{
"result-set": {
"docs": [
{
"b": [
2,
2.3010299956639813,
2.4771212547196626
],
"c": [
100,
200.00000000000003,
300.0000000000001
]
},
{
"EOF": true,
"RESPONSE_TIME": 0
}
]
}
}使用 recip 函数转换的向量可以通过取倒数的倒数来进行反向转换。
下面的示例展示了 recip 函数的反向转换示例。
let(echo="b,c",
a=array(100, 200, 300),
b=recip(a),
c=recip(b))当此表达式发送到 /stream 处理程序时,它会响应
{
"result-set": {
"docs": [
{
"b": [
0.01,
0.005,
0.0033333333333333335
],
"c": [
100,
200,
300
]
},
{
"EOF": true,
"RESPONSE_TIME": 0
}
]
}
}