概率分布

本用户指南部分介绍数学表达式库中包含的概率分布框架。

可视化

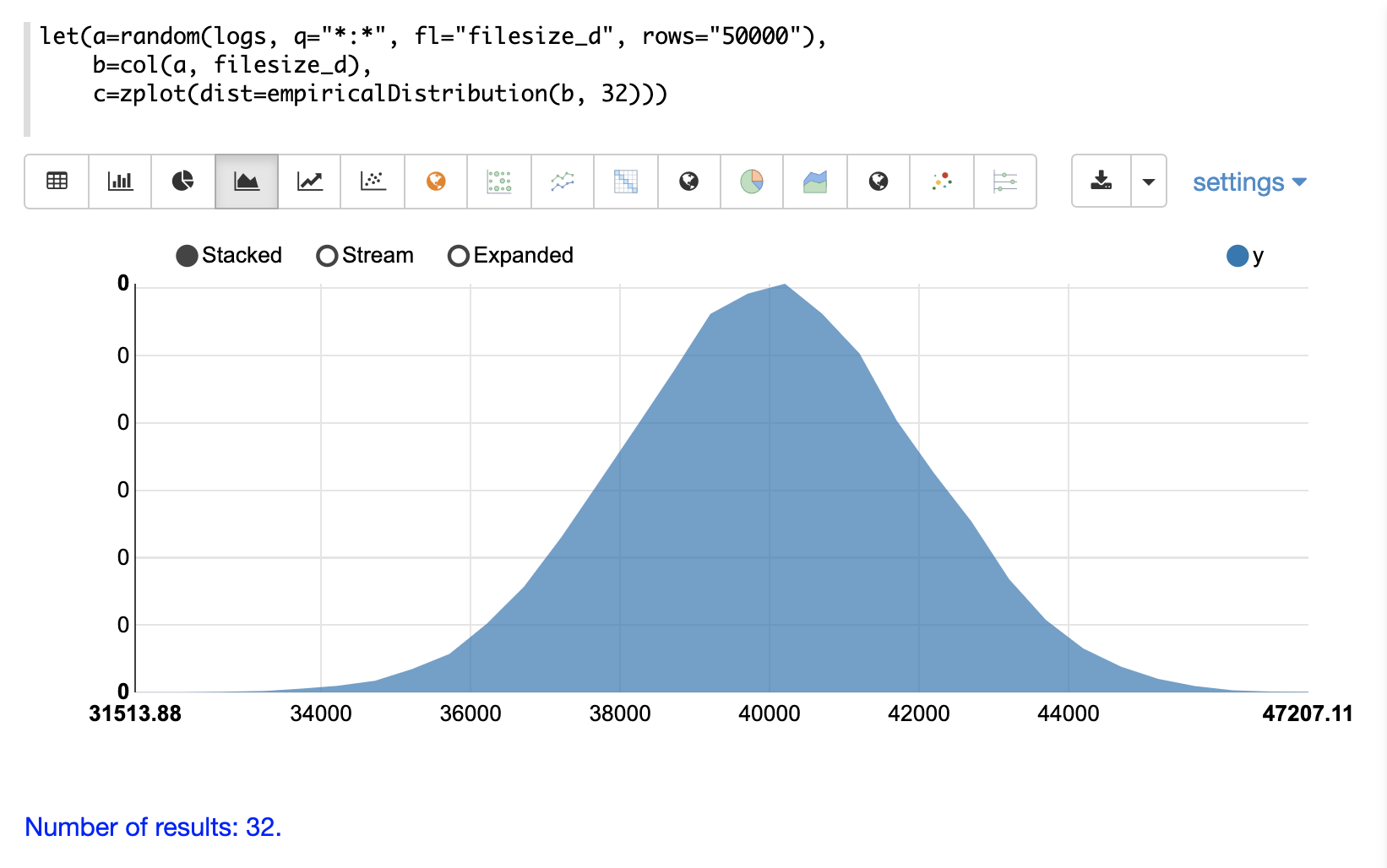
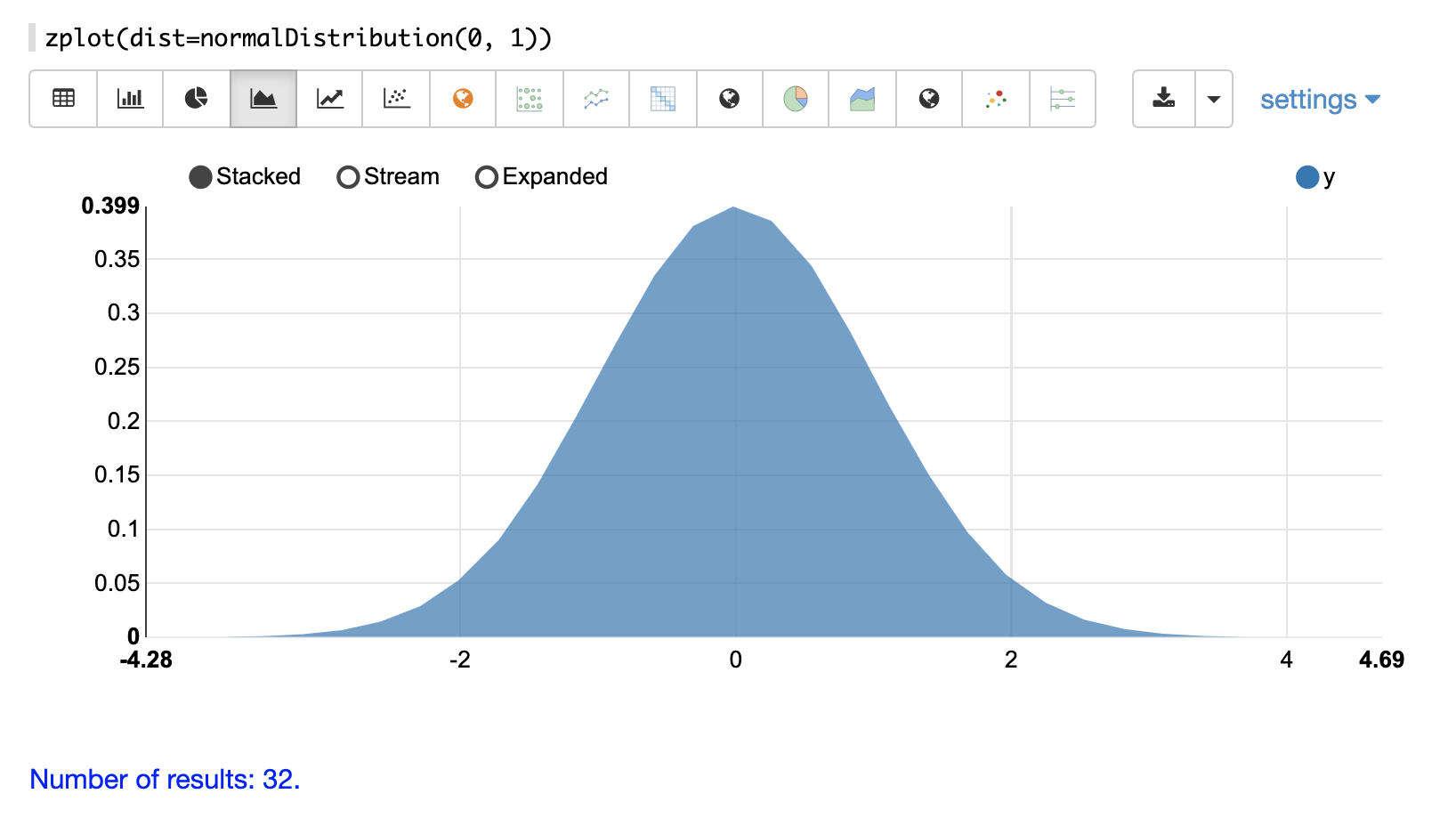
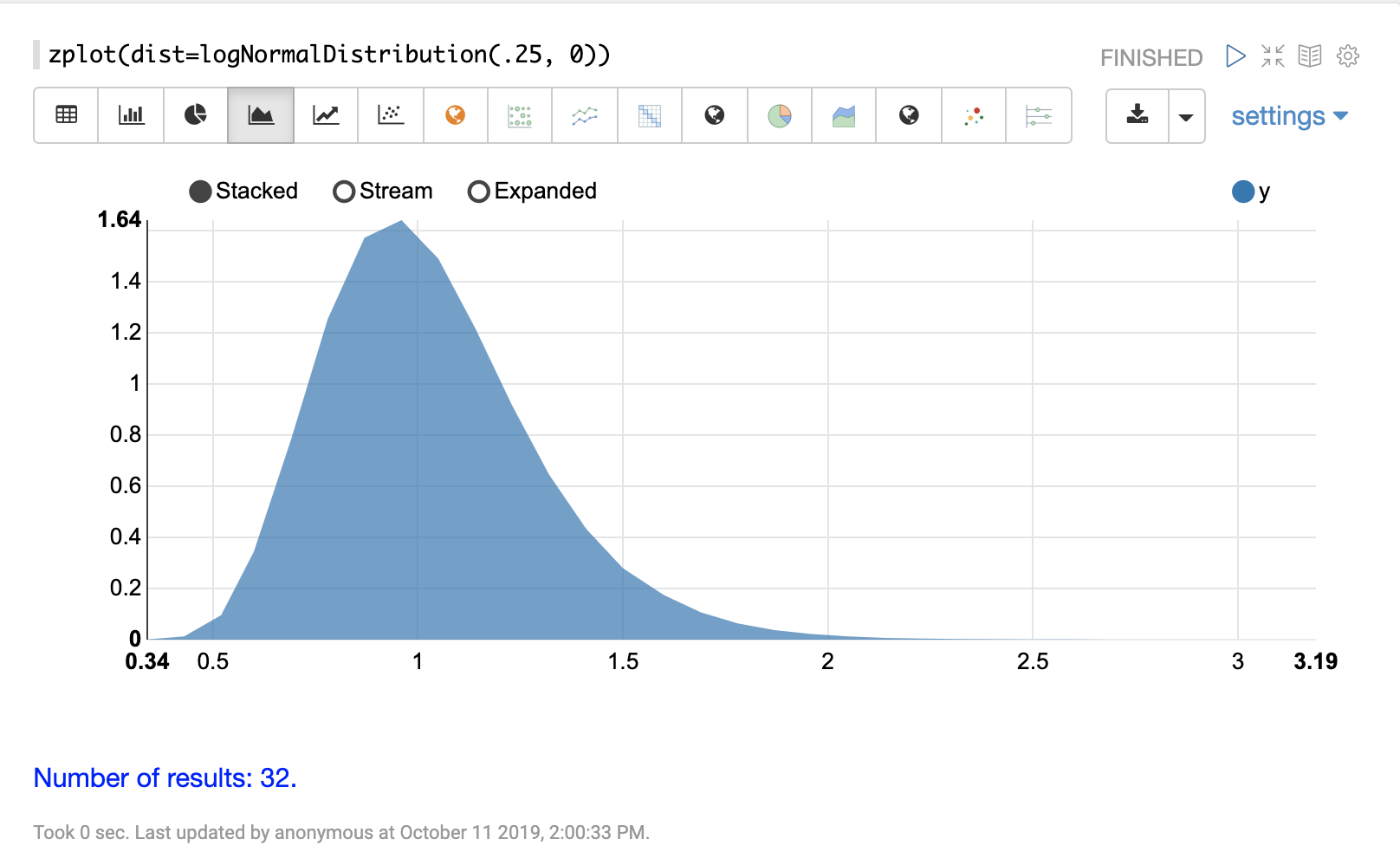
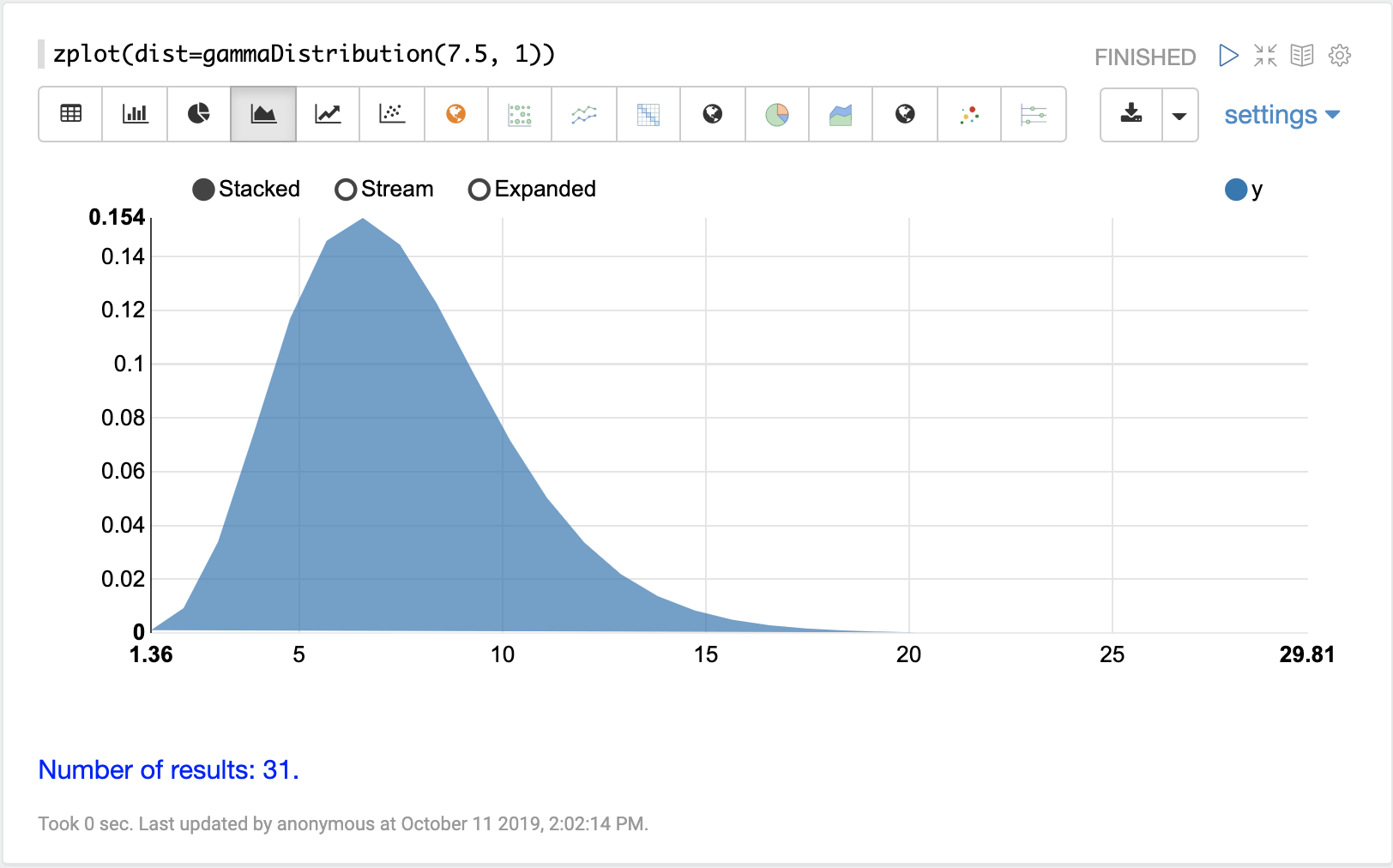
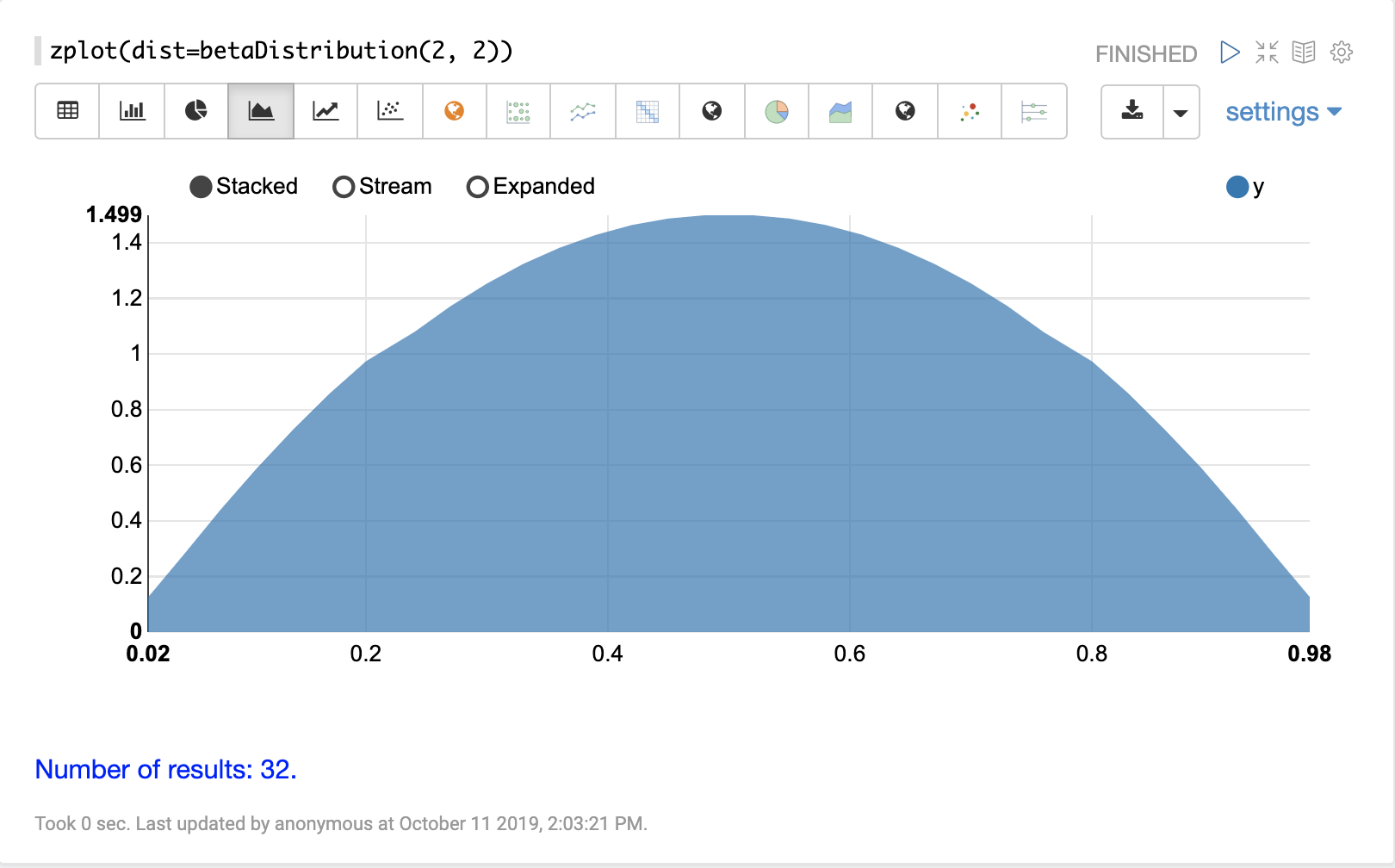
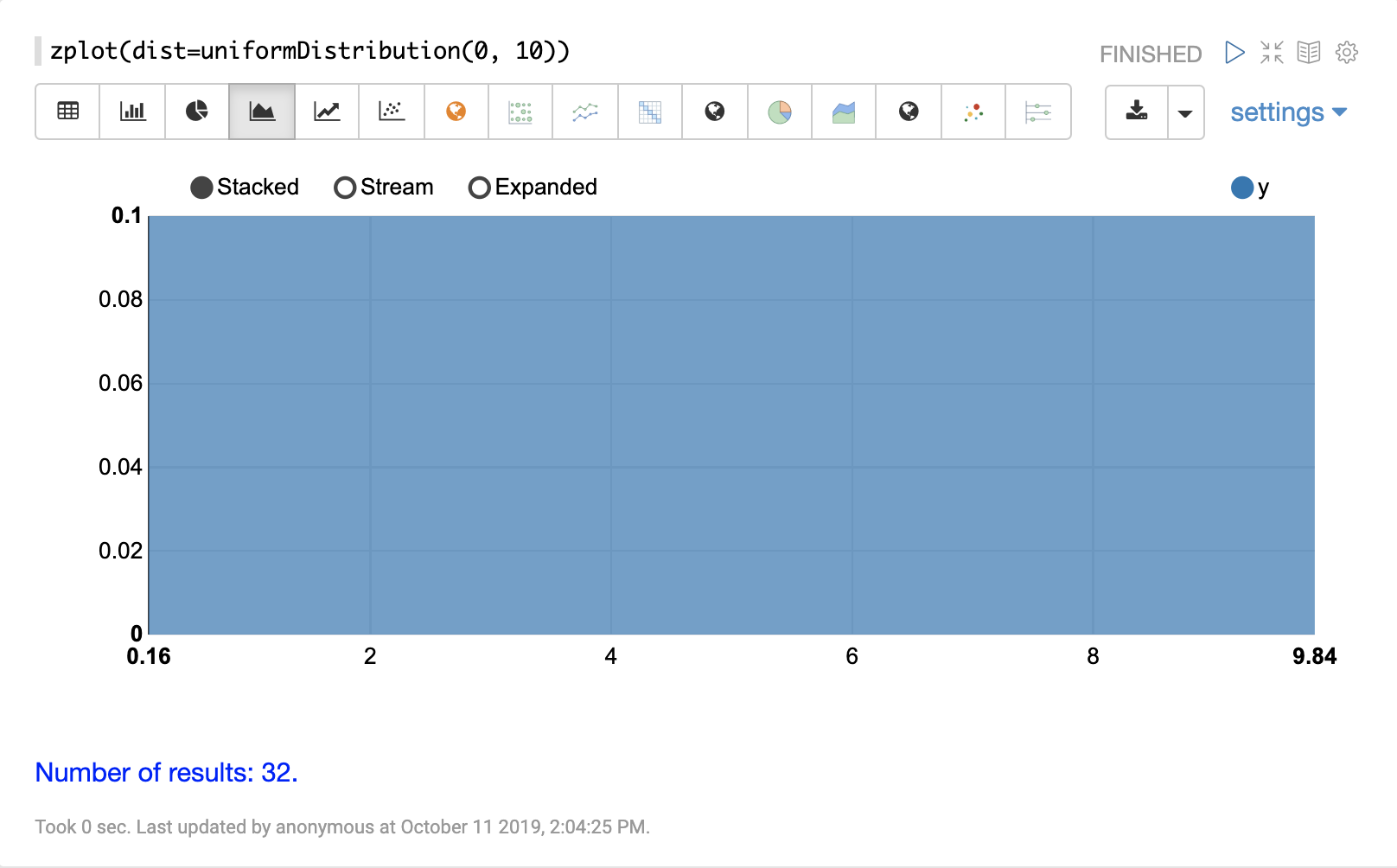
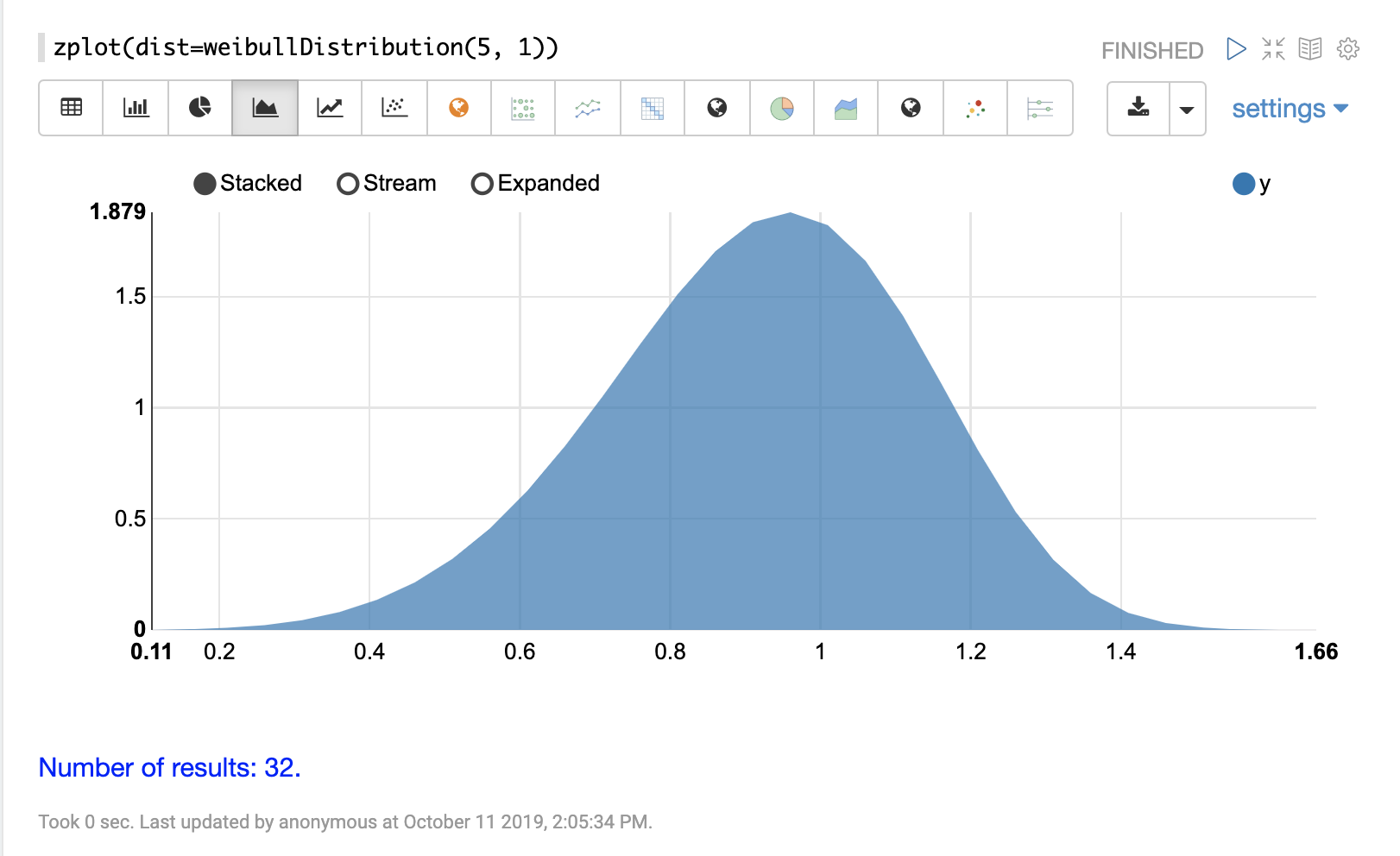
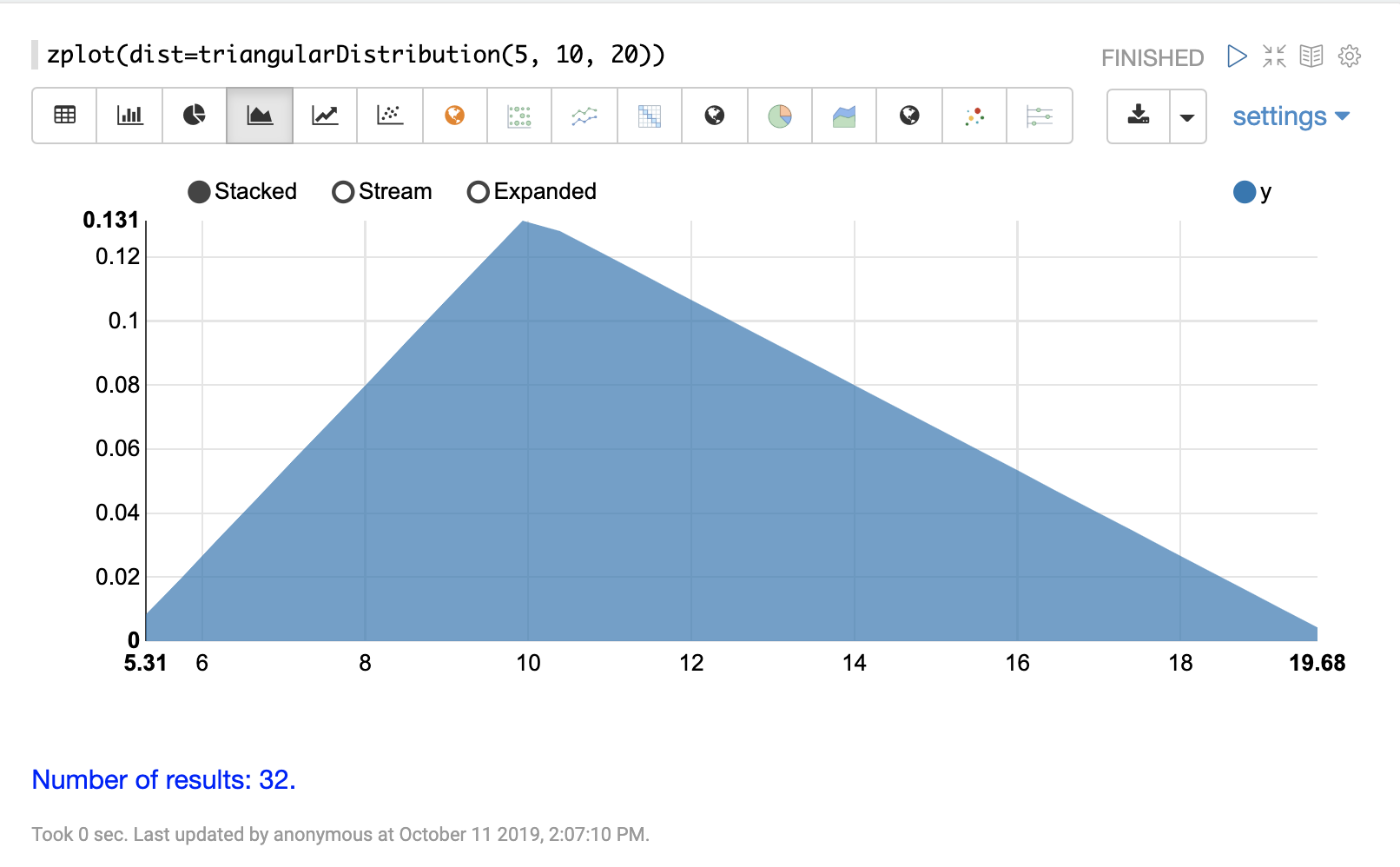
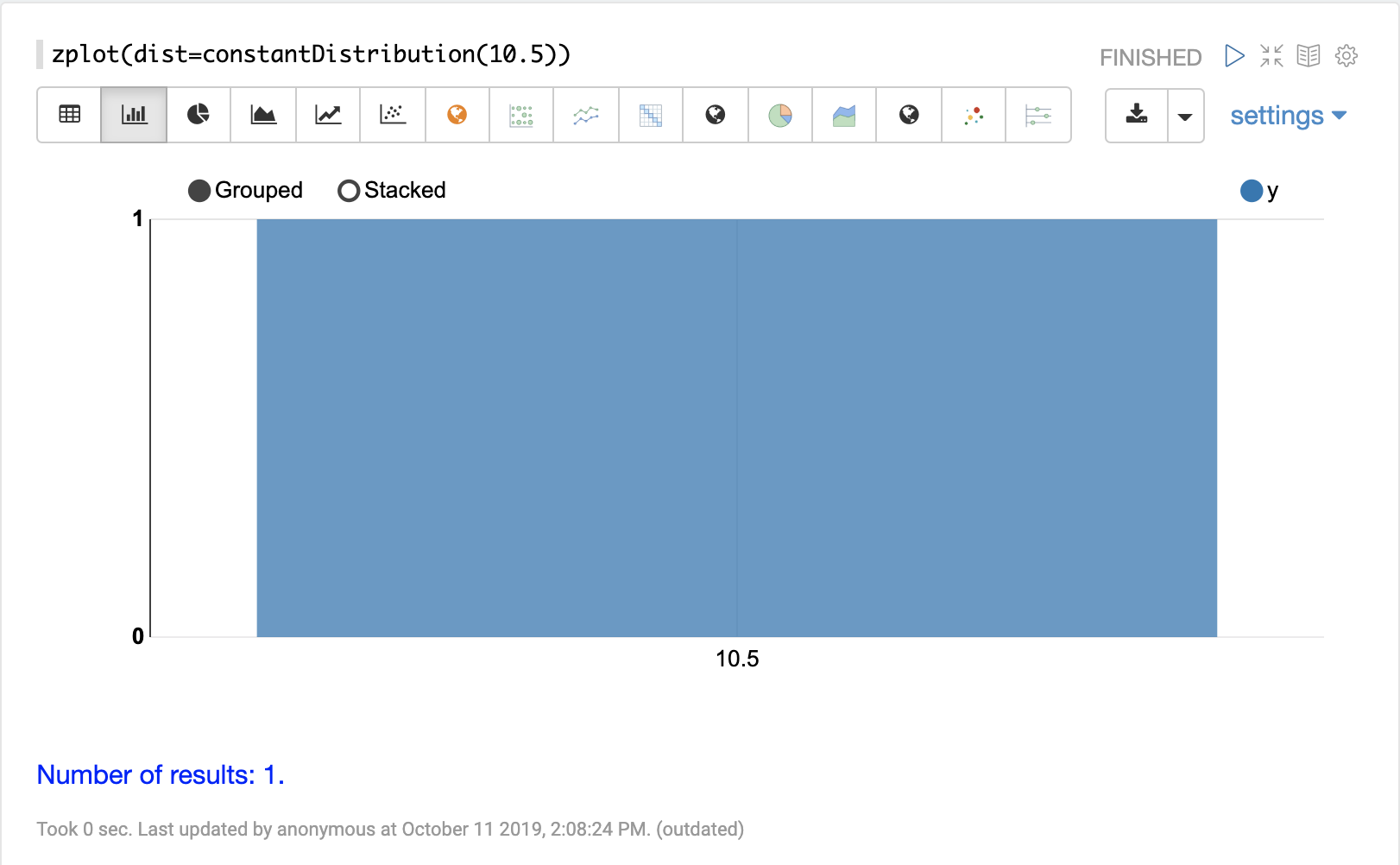
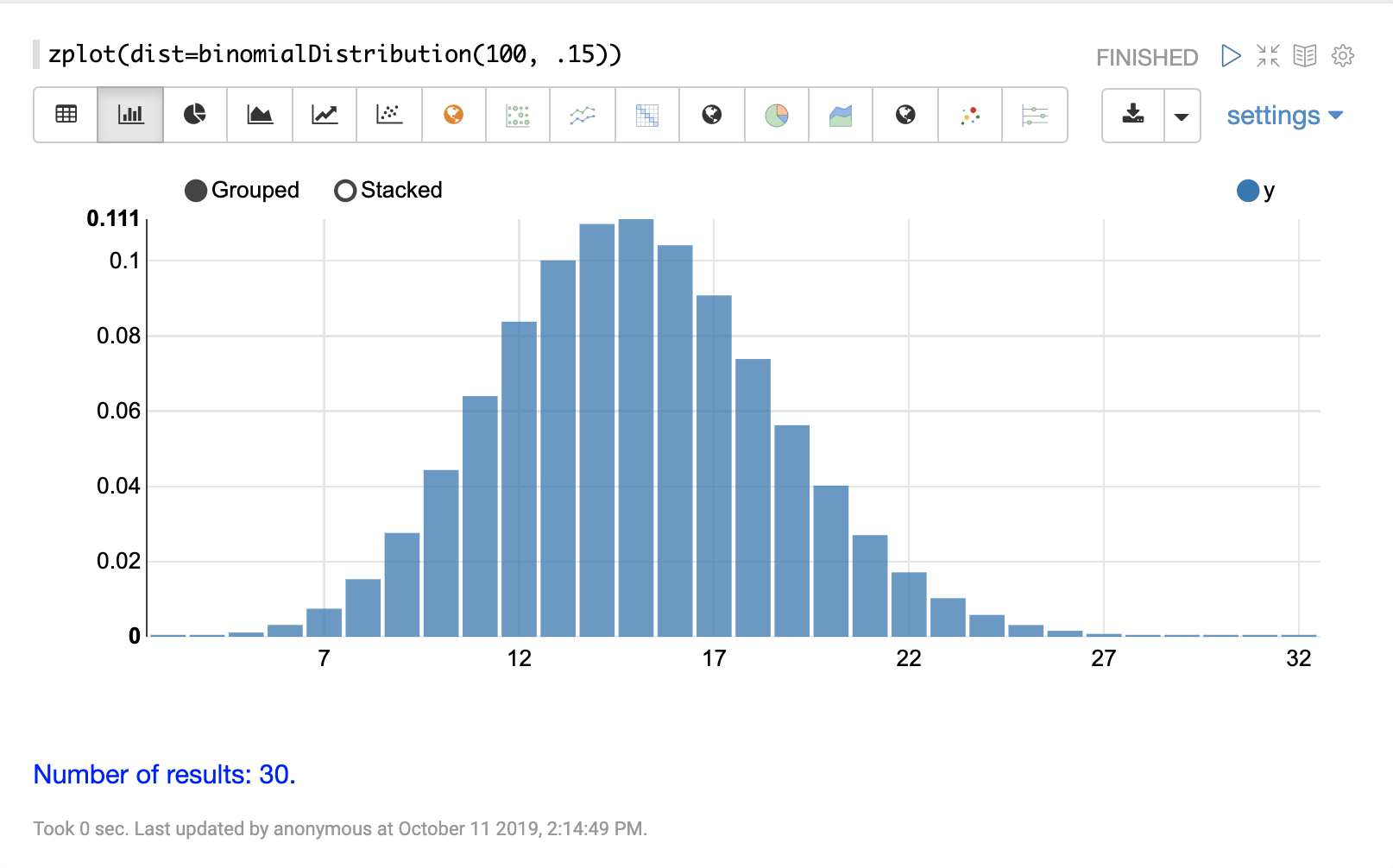
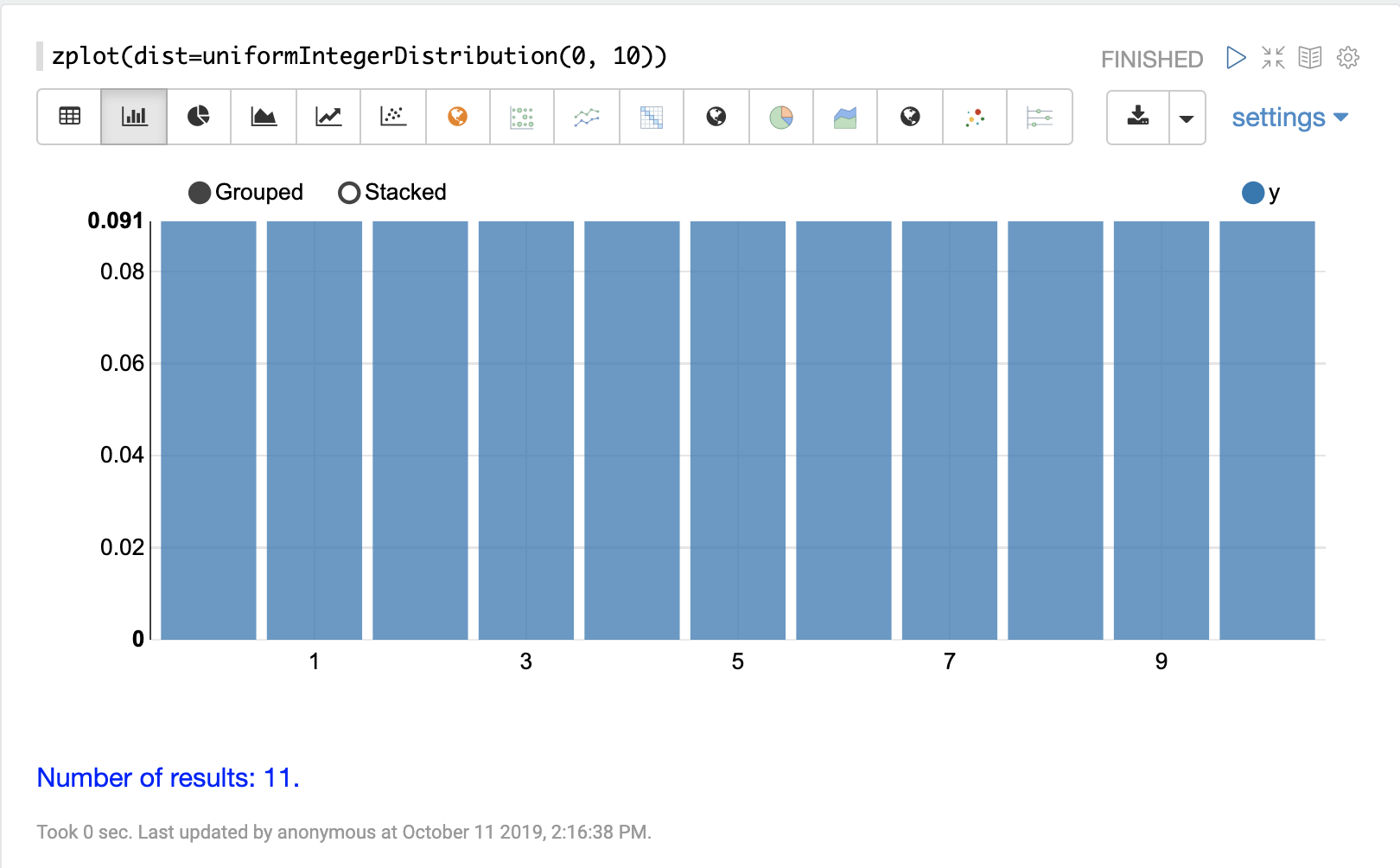
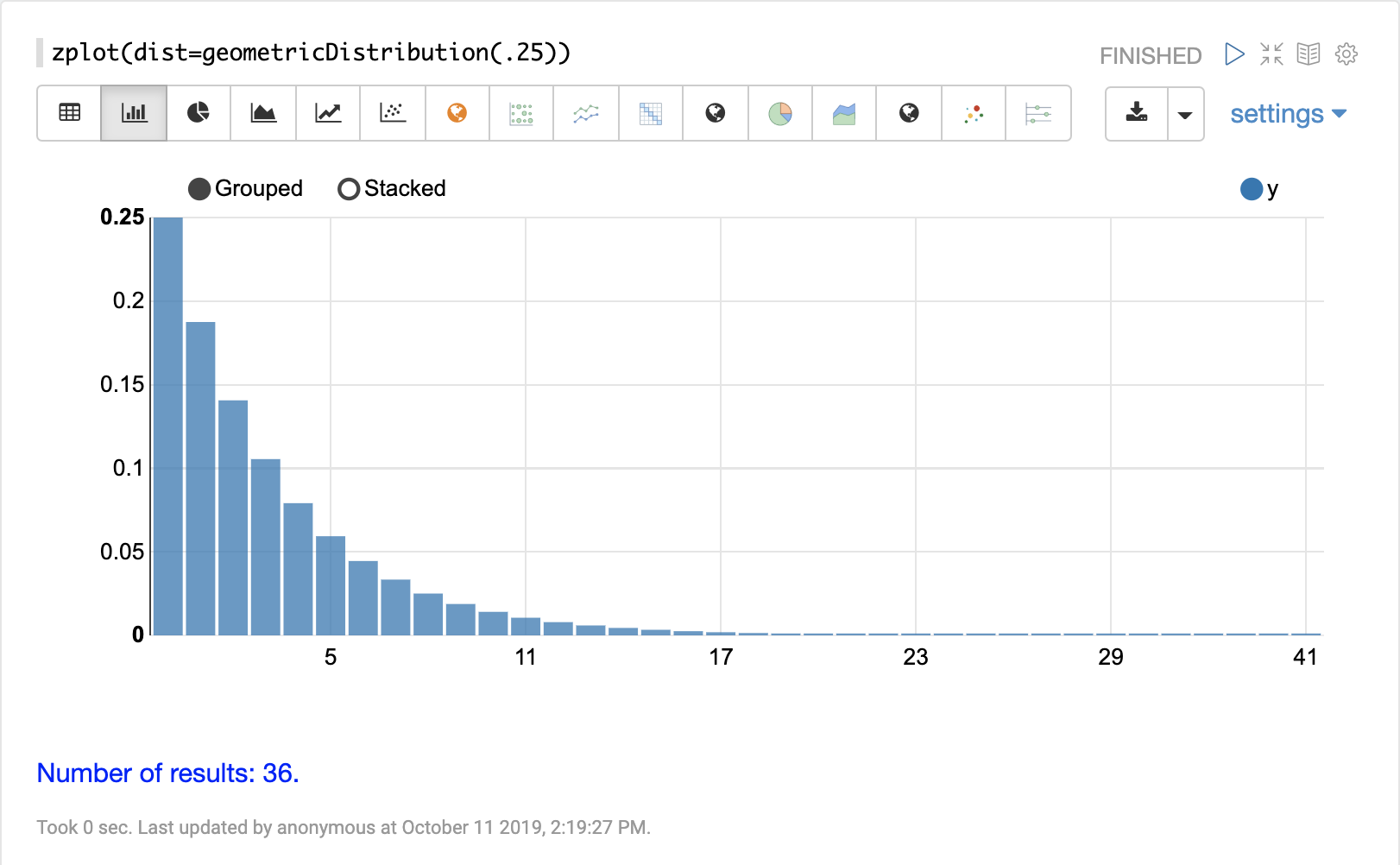
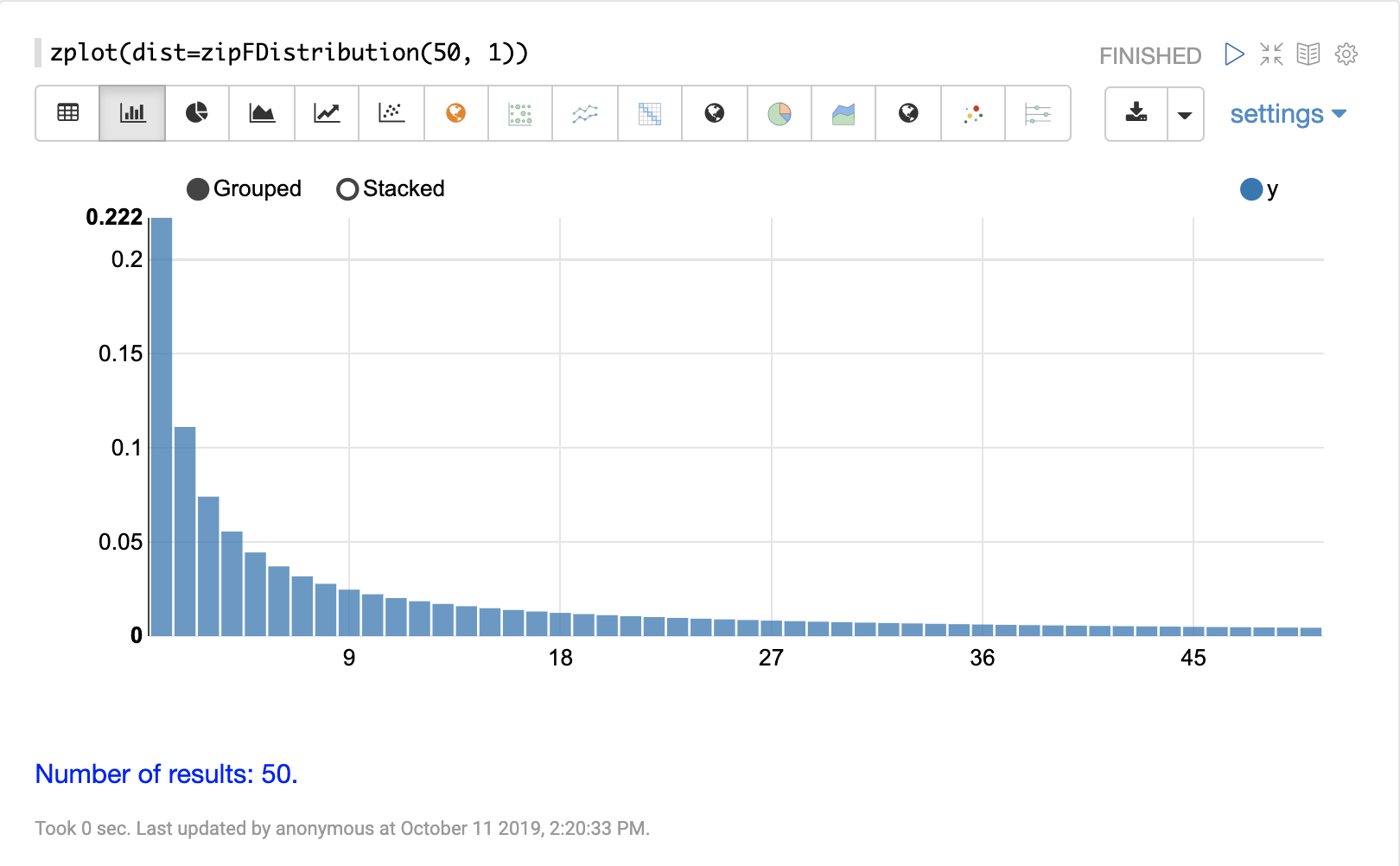
可以使用 Zeppelin-Solr 和 zplot 函数（带 dist 参数）对概率分布进行可视化，该函数可视化分布的概率密度函数 (PDF)。

每个分布的示例可视化如下所示。

连续分布

连续概率分布适用于连续数字（浮点数）。以下是支持的连续概率分布。

empiricalDistribution

empiricalDistribution 函数根据实际数据创建连续概率分布。

经验分布可用于方便地可视化来自 SolrCloud 集合的随机样本的概率密度函数。以下示例显示了 zplot 函数，该函数可视化具有 32 个 bin 直方图的随机样本的概率密度。

$empirical$

normalDistribution

以下可视化显示了均值为 0、标准差为 1 的正态分布。

$dist$

logNormalDistribution

以下可视化显示了形状为 .25、比例为 0 的对数正态分布。

$lognormal$

gammaDistribution

以下可视化显示了形状为 7.5、比例为 1 的伽马分布。

$gamma$

betaDistribution

以下可视化显示了形状 1 为 2、形状 2 为 2 的贝塔分布。

$beta$

uniformDistribution

以下可视化显示了介于 0 和 10 之间的均匀分布。

$uniformr$

weibullDistribution

以下可视化显示了形状为 5、比例为 1 的威布尔分布。

$weibull$

triangularDistribution

下方的可视化显示一个三角分布，其中低值为 5，众数为 10，高值为 20。

$triangular$

constantDistribution

下方的可视化显示一个常量分布，值为 10.5。

$constant$

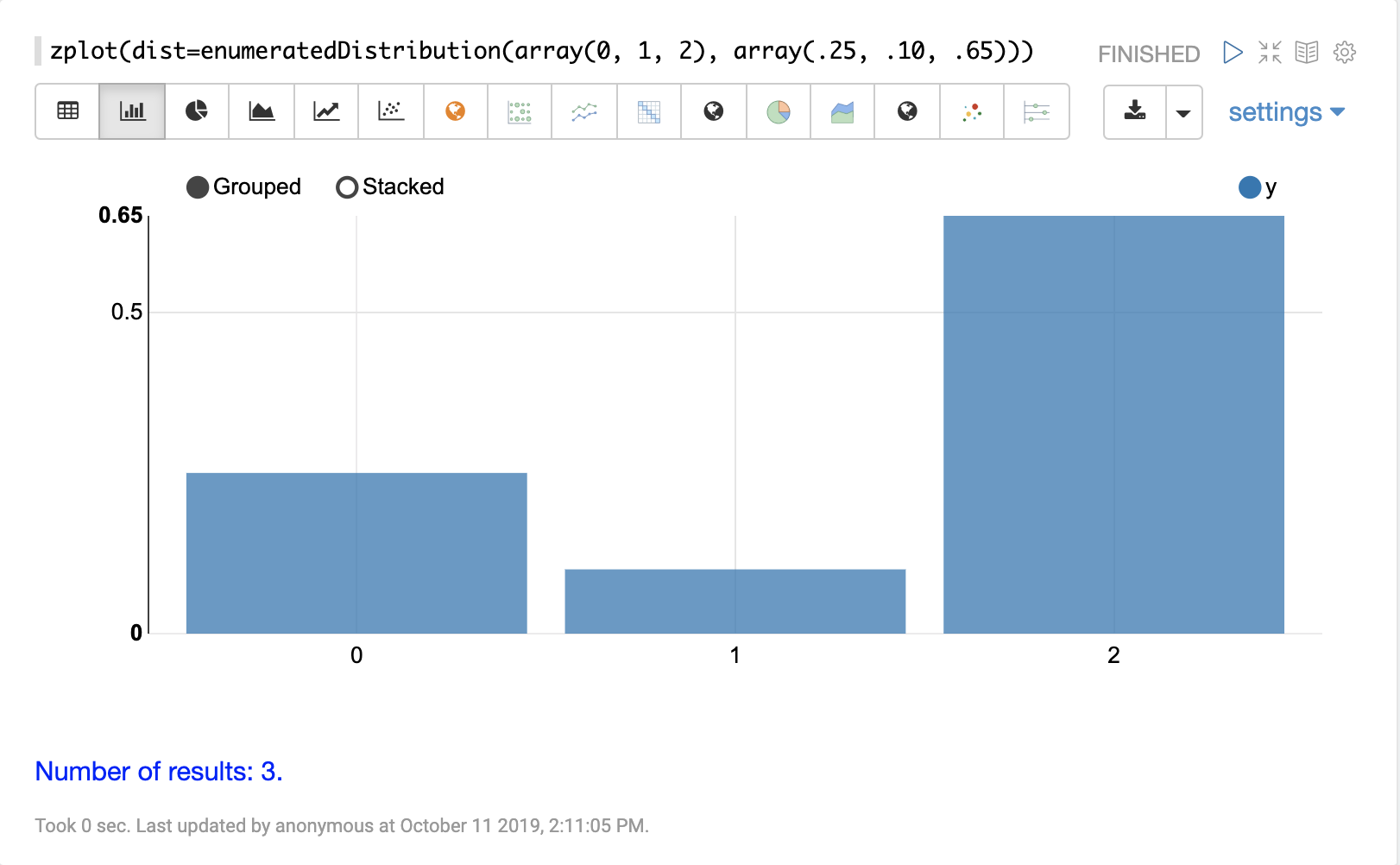
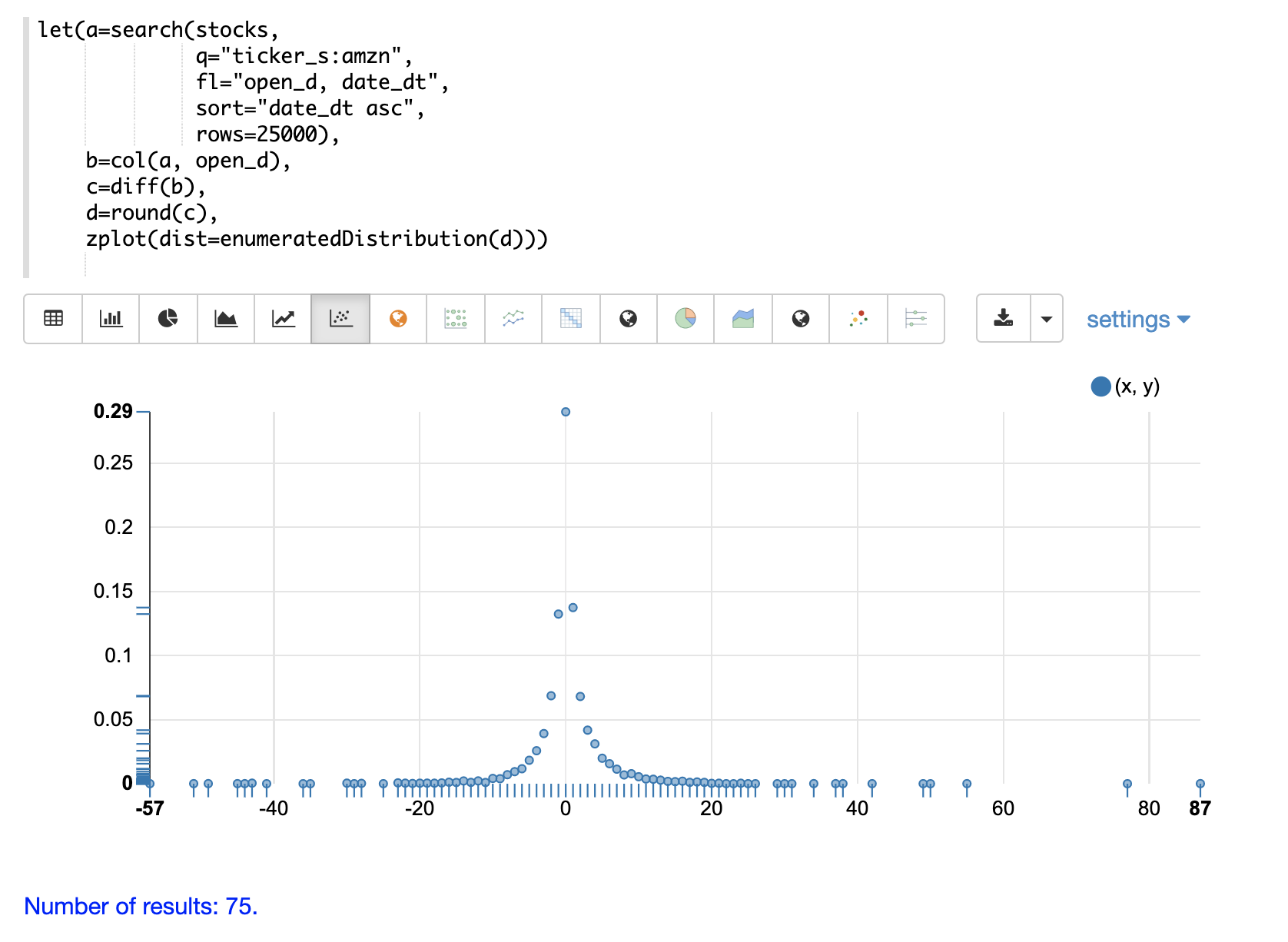
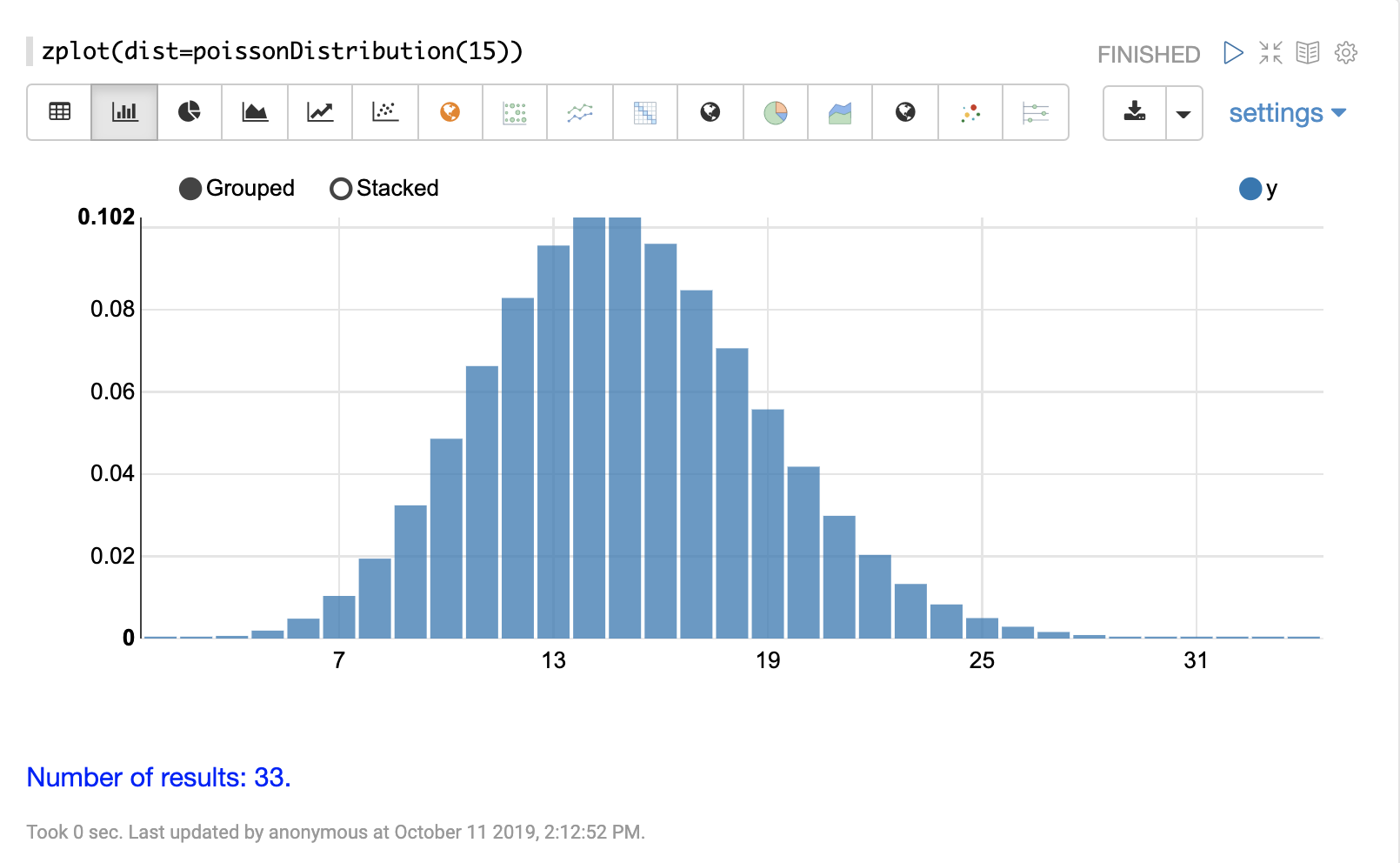
离散分布

离散概率分布适用于离散数字（整数）。以下是支持的离散概率分布。

enumeratedDistribution

enumeratedDistribution 函数从枚举值和概率列表或离散值数据集创建离散分布函数。

下方的可视化显示从离散值和概率列表创建的枚举分布。

$enum1$

下方的可视化显示从已转换为离散值向量的搜索结果生成的枚举分布。

$enum2$

poissonDistribution

下方的可视化显示一个泊松分布，其中均值为 15。

$poisson$

binomialDistribution

下方的可视化显示一个二项分布，其中试验次数为 100，成功概率为 0.15。

$binomial$

uniformIntegerDistribution

下方的可视化显示一个介于 0 和 10 之间的均匀整数分布。

$uniform$

geometricDistribution

下方的可视化显示一个几何分布，成功概率为 0.25。

$geometric$

zipFDistribution

下方的可视化显示一个 ZipF 分布，大小为 50，指数为 1。

$zipf$

累积概率

cumulativeProbability 函数可用于所有概率分布，以计算在特定分布中遇到特定随机变量的累积概率。

以下是计算正态分布中随机变量累积概率的示例。

let(a=normalDistribution(10, 5),
    b=cumulativeProbability(a, 12))

在此示例中，创建了一个正态分布函数，均值为 10，标准差为 5。然后，针对此特定分布计算值 12 的累积概率。

将此表达式发送到/stream处理程序时，它会响应

{
  "result-set": {
    "docs": [
      {
        "b": 0.6554217416103242
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 0
      }
    ]
  }
}

概率

所有概率分布都可以计算值范围之间的概率。

在以下示例中，从日志集合中抽取的文件大小样本创建了一个经验分布。然后，计算文件大小在 40000 到 41000 范围之间的概率为 19%。

let(a=random(logs, q="*:*", fl="filesize_d", rows="50000"),
    b=col(a, filesize_d),
    c=empiricalDistribution(b, 100),
    d=probability(c, 40000, 41000))

将此表达式发送到/stream处理程序时，它会响应

{
  "result-set": {
    "docs": [
      {
        "d": 0.19006540560734791
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 550
      }
    ]
  }
}

离散概率

probability 函数可用于任何离散分布函数，以计算离散值的概率。

以下是一个示例，它计算泊松分布中离散值的概率。

在示例中，使用均值为 100 的泊松分布函数创建泊松分布函数。然后，针对此特定分布计算遇到离散值 101 的样本的概率。

let(a=poissonDistribution(100),
    b=probability(a, 101))

将此表达式发送到/stream处理程序时，它会响应

{
  "result-set": {
    "docs": [
      {
        "b": 0.039466333474403106
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 0
      }
    ]
  }
}

采样

所有概率分布都支持采样。sample 函数从概率分布中返回一个或多个随机样本。

下面是一个从正态分布中绘制单个样本的示例。

let(a=normalDistribution(10, 5),
    b=sample(a))

将此表达式发送到/stream处理程序时，它会响应

{
  "result-set": {
    "docs": [
      {
        "b": 11.24578055004963
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 0
      }
    ]
  }
}

采样函数还可以返回样本向量。样本向量可以可视化为散点图，以直观地了解底层分布。

第一个示例显示均值为 0、标准差为 5 的正态分布的散点图。

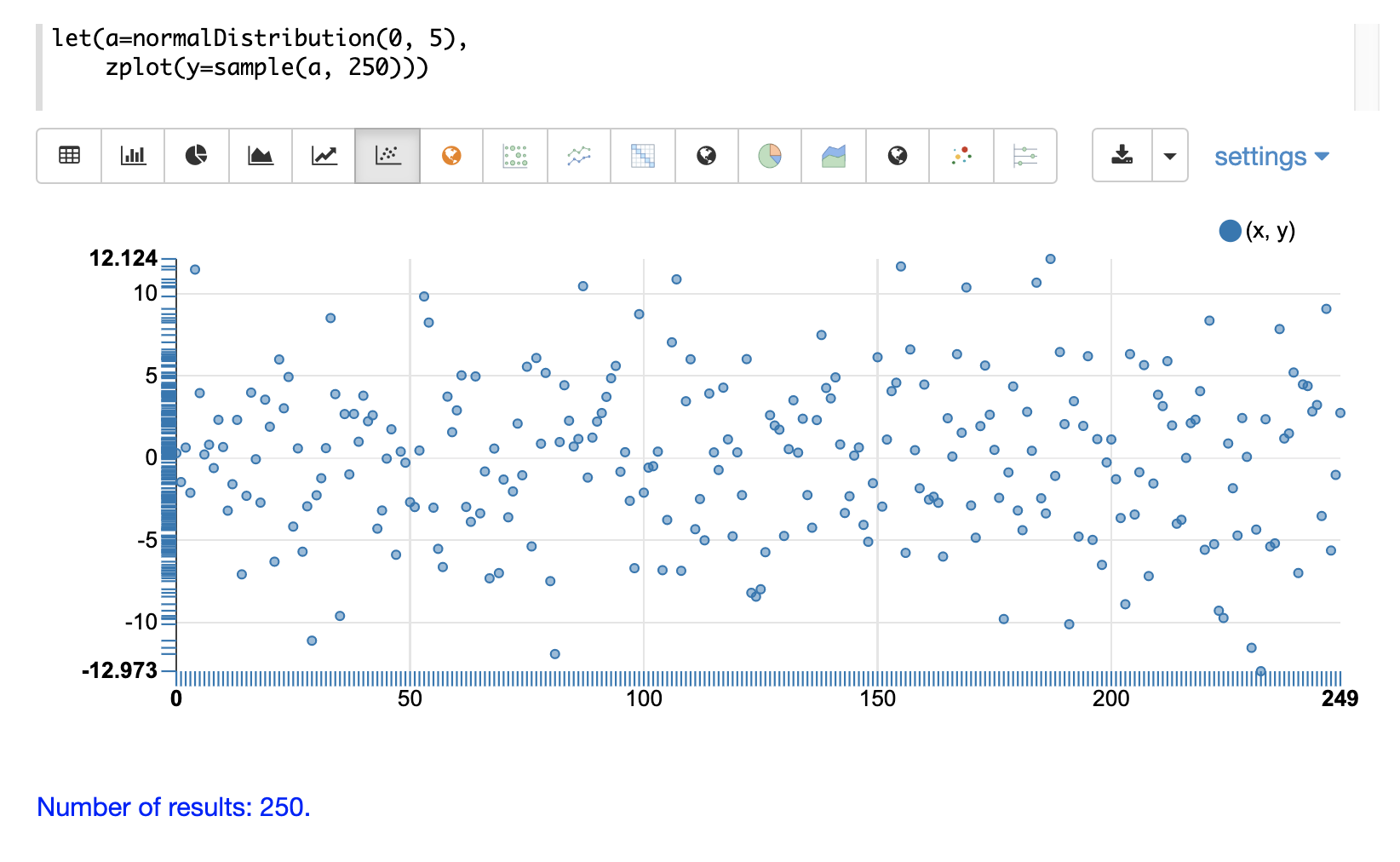
$sample scatter$

下一个示例显示了对样本向量应用升序排序的相同分布的散点图。

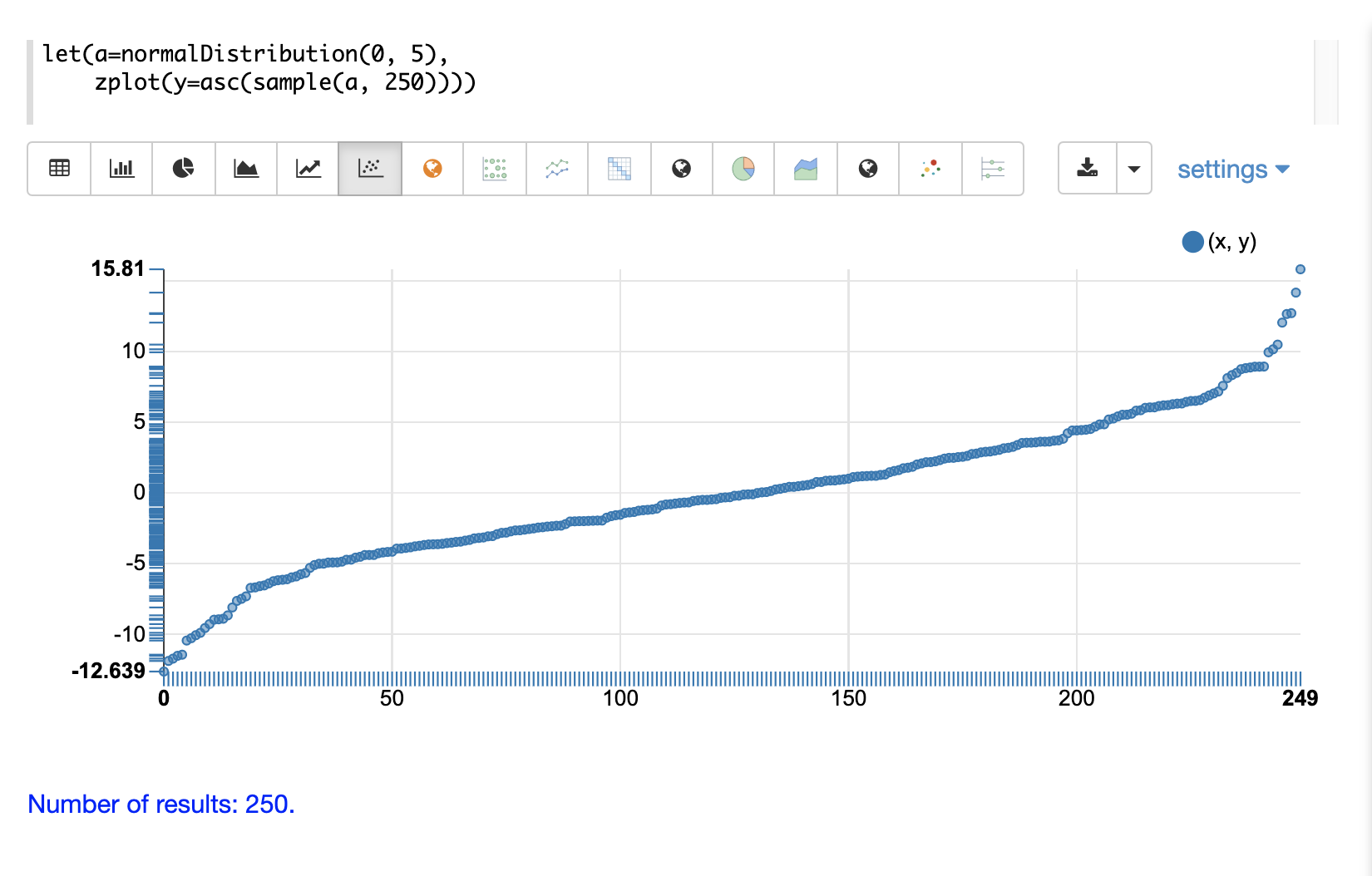
$sample scatter1$

下一个示例显示了在同一散点图中叠加的两个不同的分布。

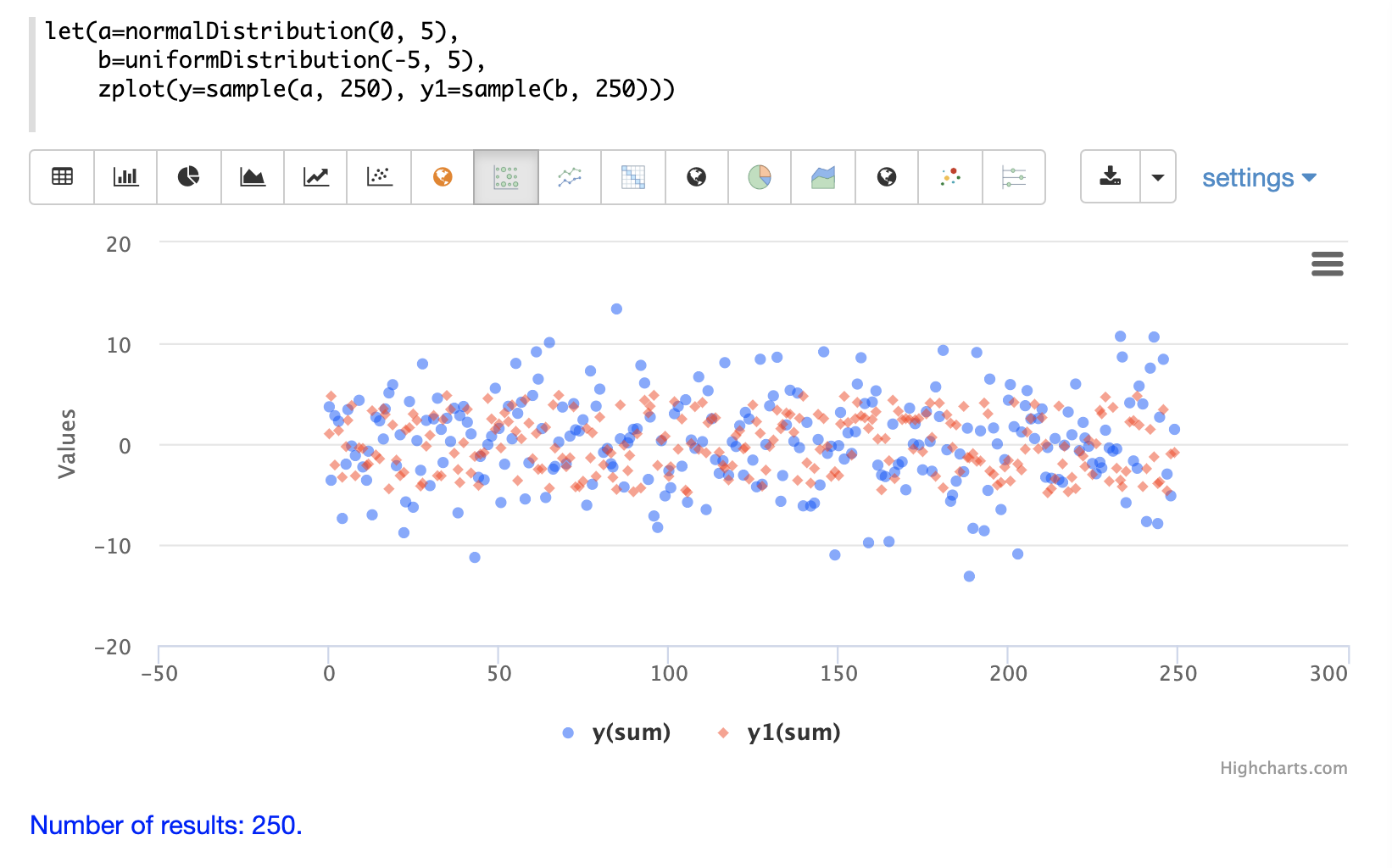
$sample overlay$

多元正态分布

多元正态分布是一元正态分布向更高维度的推广。

多元正态分布对两个或更多个正态分布的随机变量进行建模。变量之间的关系由协方差矩阵定义。

采样

sample 函数可用于从多元正态分布中绘制样本，其方式与一元正态分布非常相似。

不同之处在于，每个样本将是一个包含从每个底层正态分布中绘制的样本的数组。如果绘制多个样本，则 sample 函数将返回一个矩阵，其中每一行都有一个样本。从长远来看，样本矩阵的列将符合用于参数化多元正态分布的协方差矩阵。

以下示例演示如何初始化和从多元正态分布中绘制样本。

在此示例中，从日志记录集合中选择了 5000 个随机样本。每个样本都包含字段 filesize_d 和 response_d。这两个字段的值都符合正态分布。

然后对这两个字段进行向量化。filesize_d 向量存储在变量 b 中，response_d 变量存储在变量 c 中。

创建一个包含这两个向量化字段的均值的数组。

然后将这两个向量添加到一个转置的矩阵中。这将创建一个观测矩阵，其中每行包含 filesize_d 和 response_d 的一个观测值。然后使用 cov 函数从观测矩阵的列创建协方差矩阵。协方差矩阵描述了 filesize_d 和 response_d 之间的协方差。

然后使用这两个字段的均值数组和协方差矩阵调用 multivariateNormalDistribution 函数。多元正态分布的模型分配给变量 g。

最后，从多元正态分布中抽取五个样本。

let(a=random(logs, q="*:*", rows="5000", fl="filesize_d, response_d"),
    b=col(a, filesize_d),
    c=col(a, response_d),
    d=array(mean(b), mean(c)),
    e=transpose(matrix(b, c)),
    f=cov(e),
    g=multiVariateNormalDistribution(d, f),
    h=sample(g, 5))

样本以矩阵的形式返回，其中每一行表示一个样本。矩阵中有两列。第一列包含 filesize_d 的样本，第二列包含 response_d 的样本。从长远来看，列之间的协方差将符合用于实例化多元正态分布的协方差矩阵。

{
  "result-set": {
    "docs": [
      {
        "h": [
          [
            41974.85669321393,
            779.4097049705296
          ],
          [
            42869.19876441414,
            834.2599296790783
          ],
          [
            38556.30444839889,
            720.3683470060988
          ],
          [
            37689.31290928216,
            686.5549428100018
          ],
          [
            40564.74398214547,
            769.9328090774
          ]
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 162
      }
    ]
  }
}