曲线拟合

polyfit 函数是一个通用曲线拟合器，用于对两个随机变量之间的非线性关系进行建模。

polyfit 函数传递 x 轴和 y 轴，并为数据拟合一条平滑曲线。如果仅提供一个数组，则将其视为 y 轴，并为 x 轴生成一个序列。可以添加第三个参数来指定多项式的阶数。如果未提供阶数，则默认使用 3 阶多项式。阶数越高，可以建模的曲线就越多。

polyfit 函数可以用与 Zeppelin-Solr 中的线性回归类似的方式可视化。

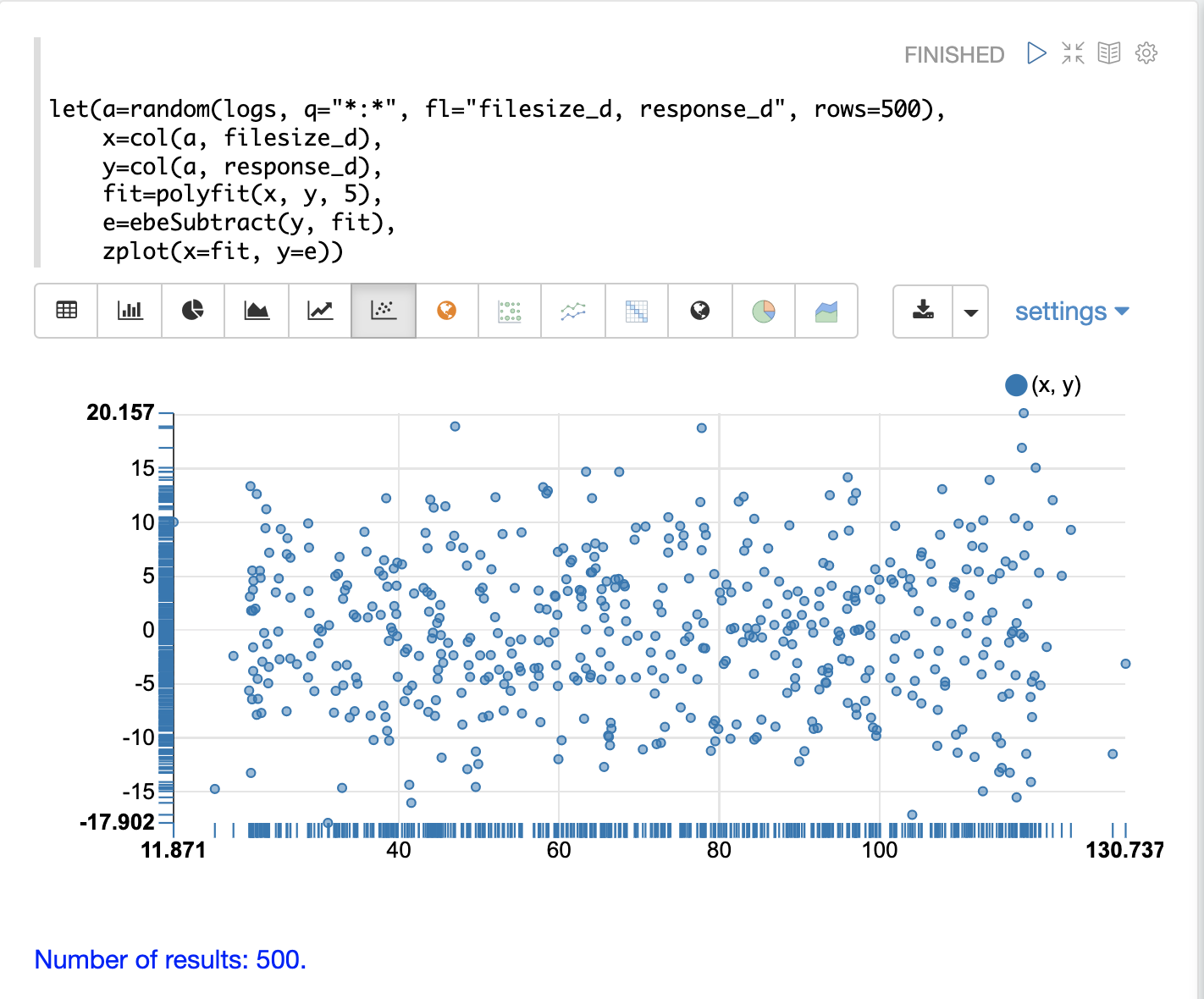
以下示例使用 polyfit 函数为随机样本的散点图拟合非线性曲线。蓝点是原始观测值的散点图，红点是预测曲线。

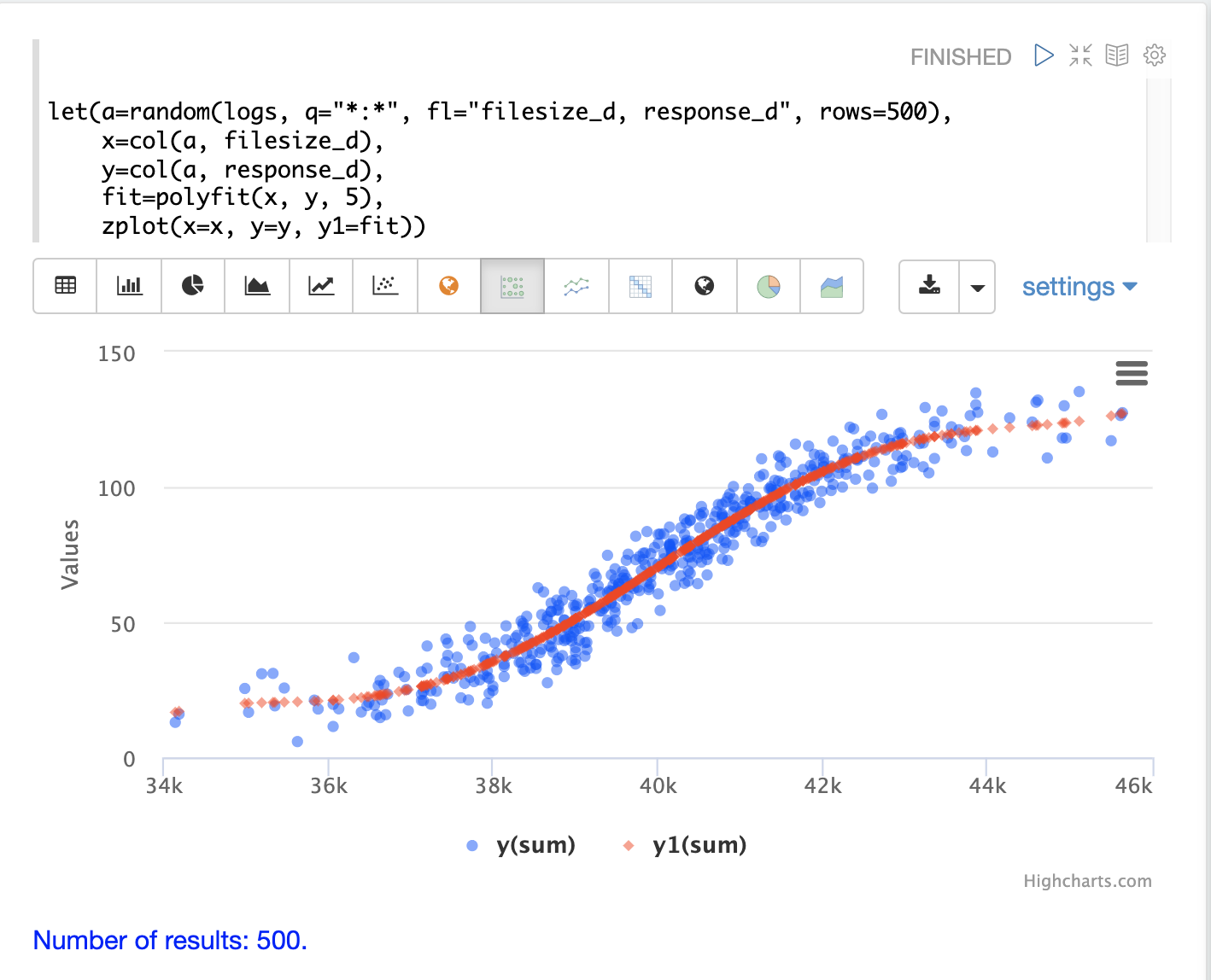
在上面的示例中，从 logs 集合中抽取包含两个字段（filesize_d 和 response_d）的随机样本。这两个字段被矢量化并设置为变量 x 和 y。

然后使用 polyfit 函数使用 5 阶多项式为数据拟合非线性模型。polyfit 函数返回一个模型，然后由 zplot 直接绘制该模型以及原始观测值。

拟合模型也可以与线性回归中一样由 predict 函数使用。以下示例使用拟合模型预测文件大小为 42000 的响应时间。

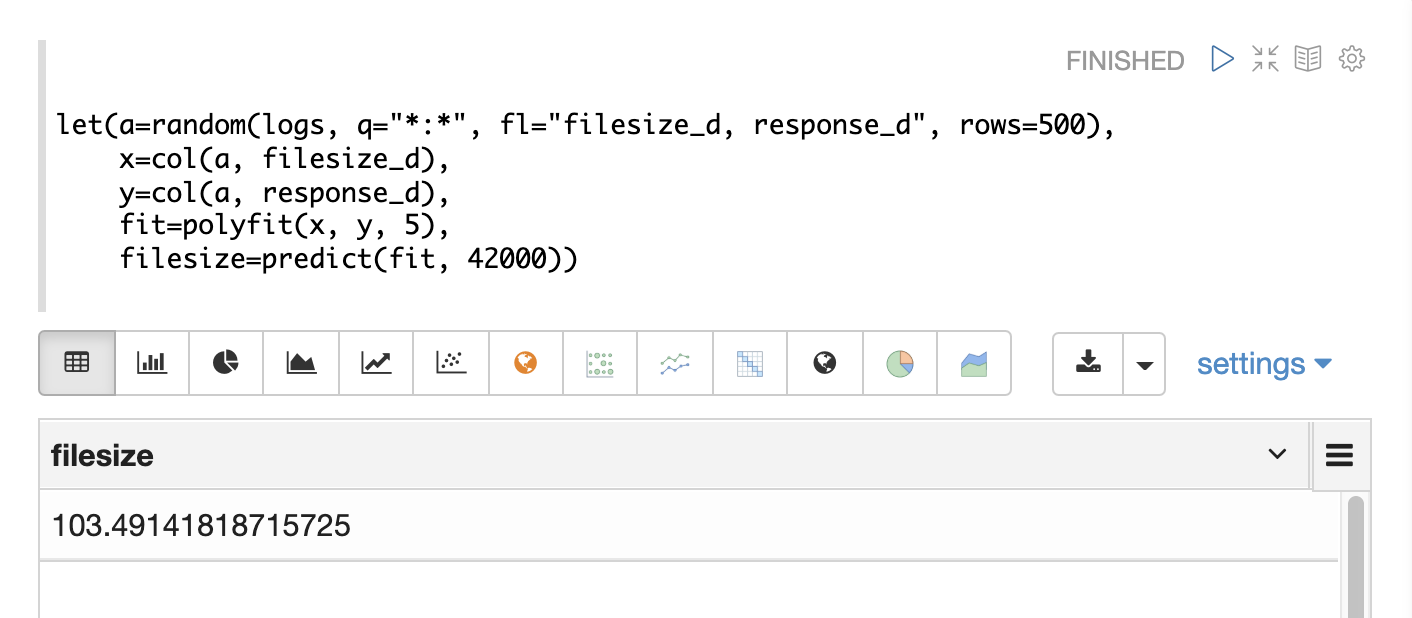
如果提供一个预测值数组，则将返回一个预测数组。

polyfit 模型执行插值和外推，这意味着它可以在数据集的范围内和范围之外预测结果。

gaussfit 函数通过高斯峰拟合平滑曲线。gaussfit 函数采用 x 轴和 y 轴，并为数据拟合平滑的高斯曲线。如果仅传递一个数字向量，gaussfit 将其视为 y 轴，并将为 x 轴生成一个序列。

gaussfit 的一个有趣用例是可视化回归模型的残差如何拟合正态分布。

拟合良好的回归模型的一个特征是其残差理想情况下将拟合正态分布。我们可以通过构建残差的直方图，然后为直方图曲线拟合高斯曲线来测试这一点。

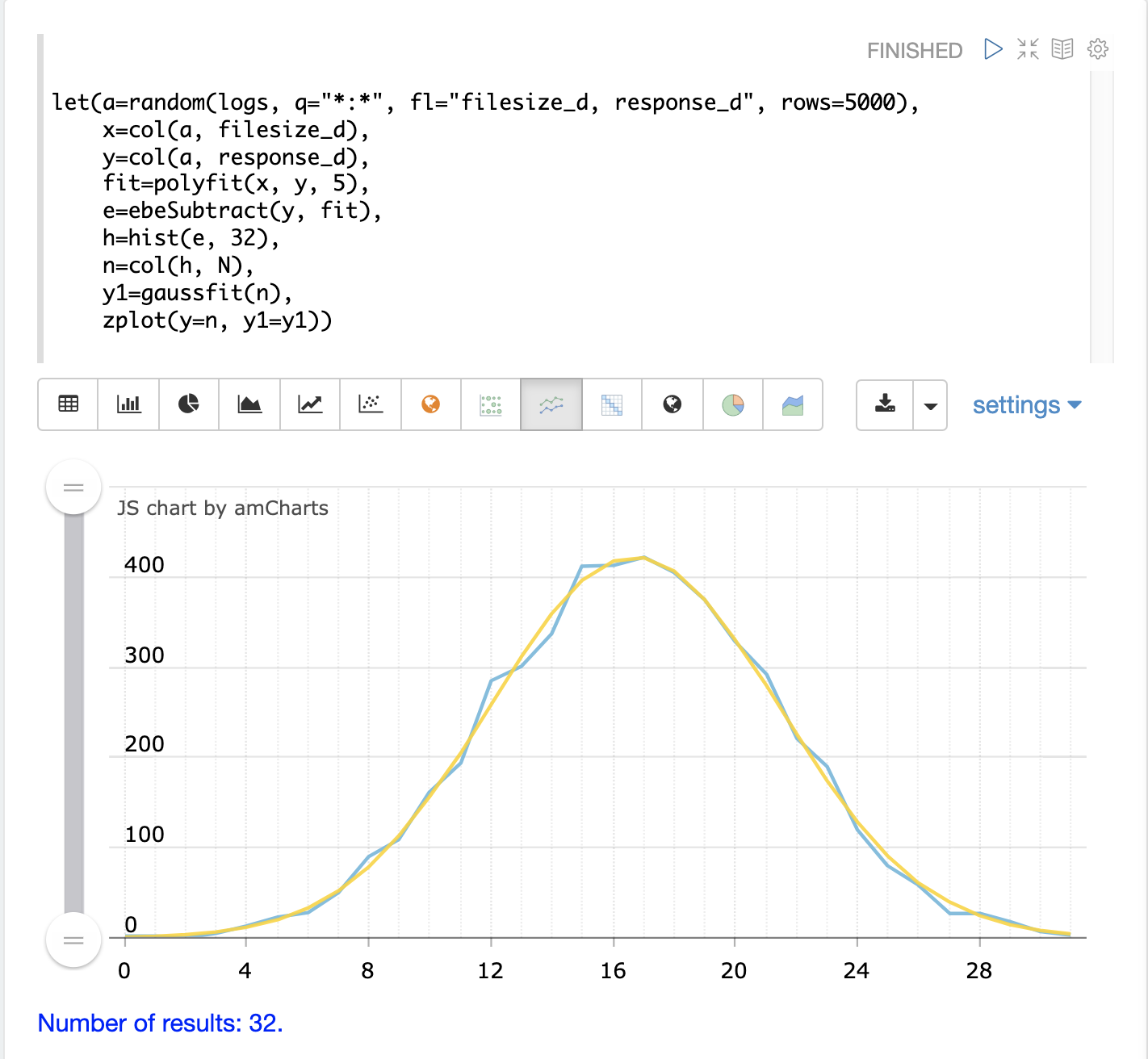
在下面的示例中，polyfit 回归的残差使用 hist 函数建模，以返回具有 32 个箱的直方图。hist 函数返回一个元组列表，其中包含有关每个箱的统计信息。在示例中，col 函数用于返回一个向量，其中包含每个箱的 N 列，即箱中的观察值计数。如果残差呈正态分布，我们希望箱计数大致遵循高斯曲线。

然后将箱计数向量作为 y 轴传递给 gaussfit。gaussfit 为 x 轴生成一个序列，然后为数据拟合高斯曲线。

然后使用 zplot 绘制原始箱计数和拟合曲线。在下面的示例中，蓝线是箱计数，平滑的黄线是拟合曲线。我们可以看到，箱形残差相当好地拟合正态分布。

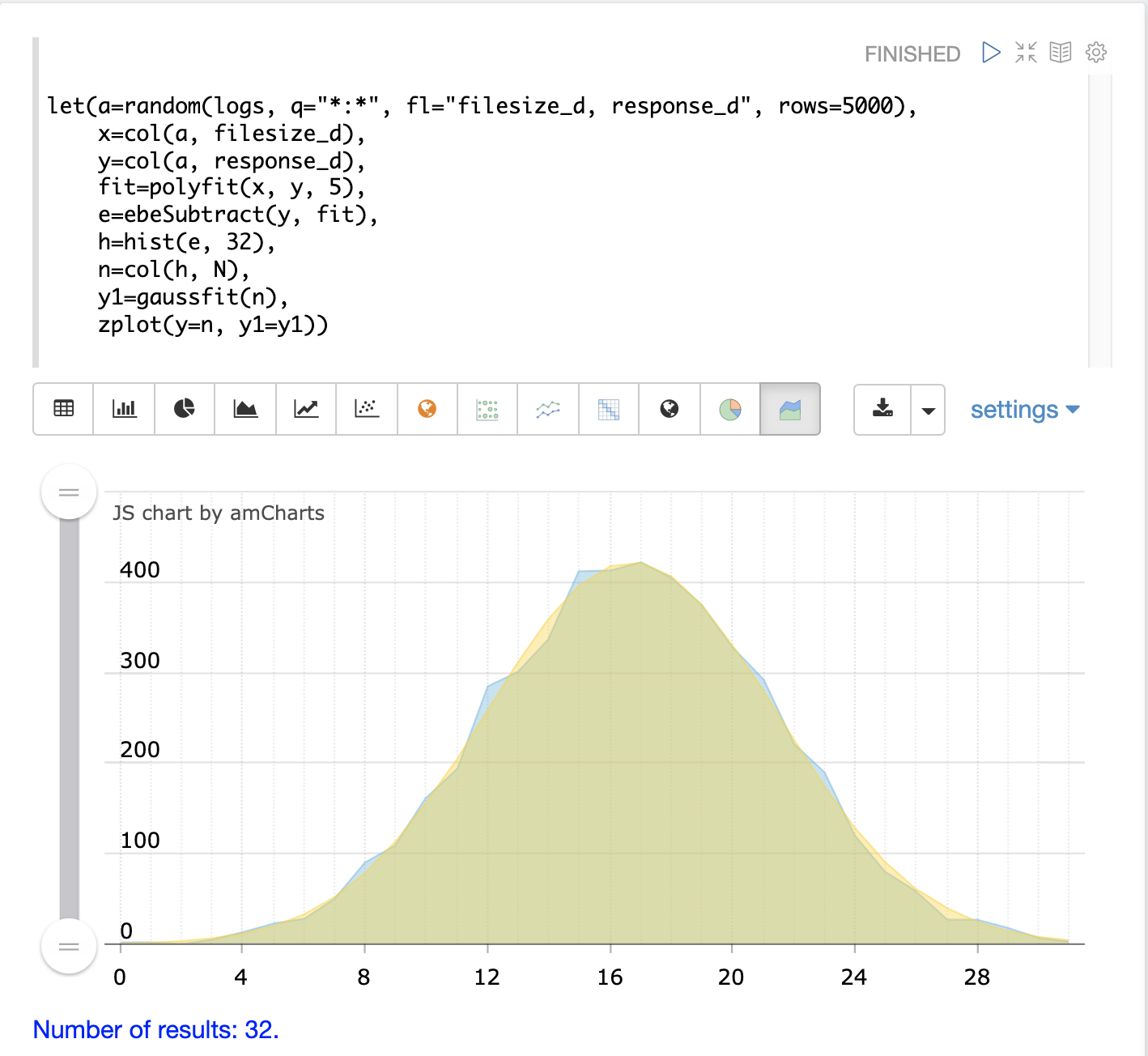
第二个图显示了两个曲线叠加在面积图上

harmonicFit 函数（或简称 harmfit）通过正弦波控制点的平滑线拟合。harmfit 函数传递 x 轴和 y 轴，并为数据拟合平滑曲线。如果提供单个数组，则将其视为 y 轴，并为 x 轴生成一个序列。

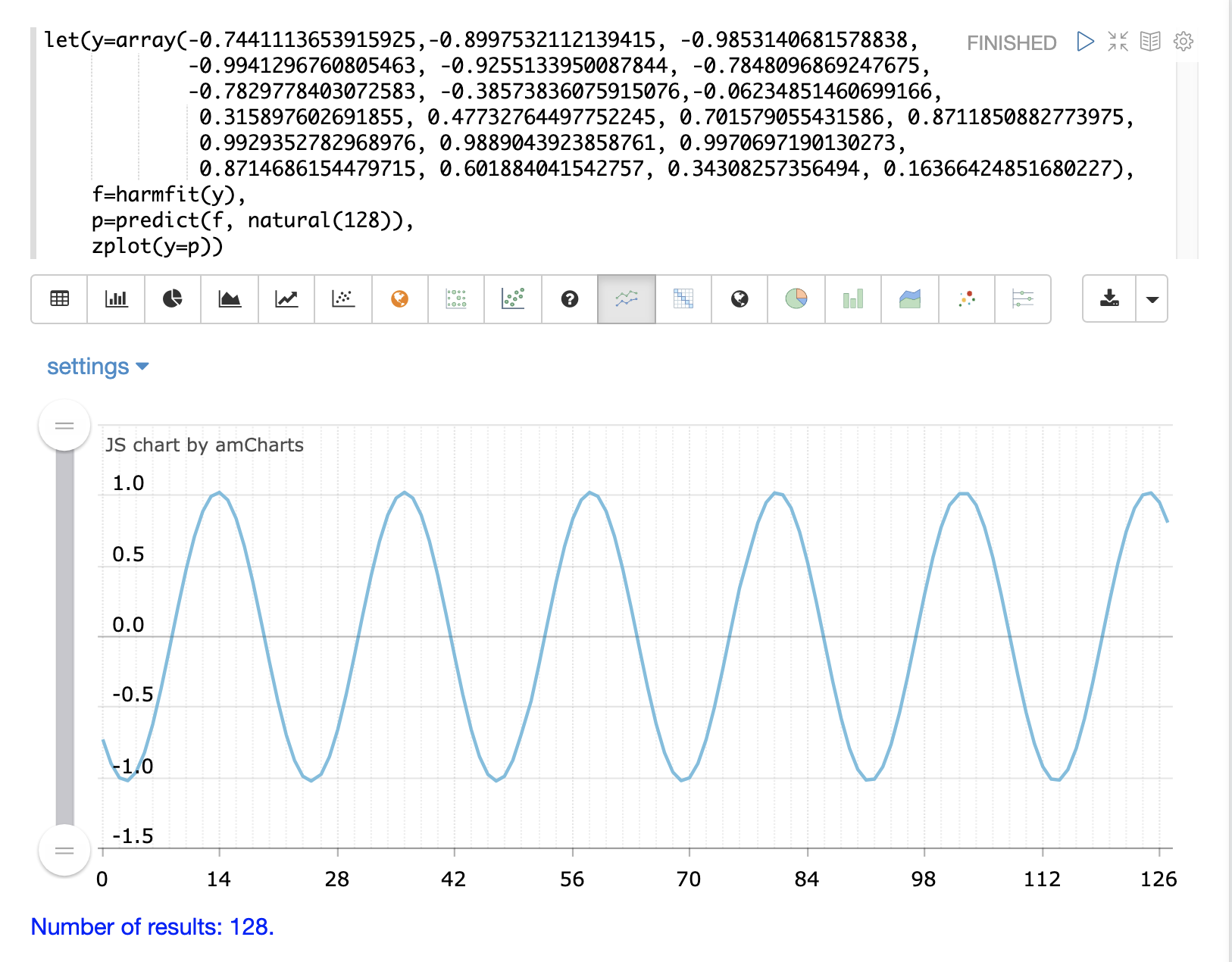
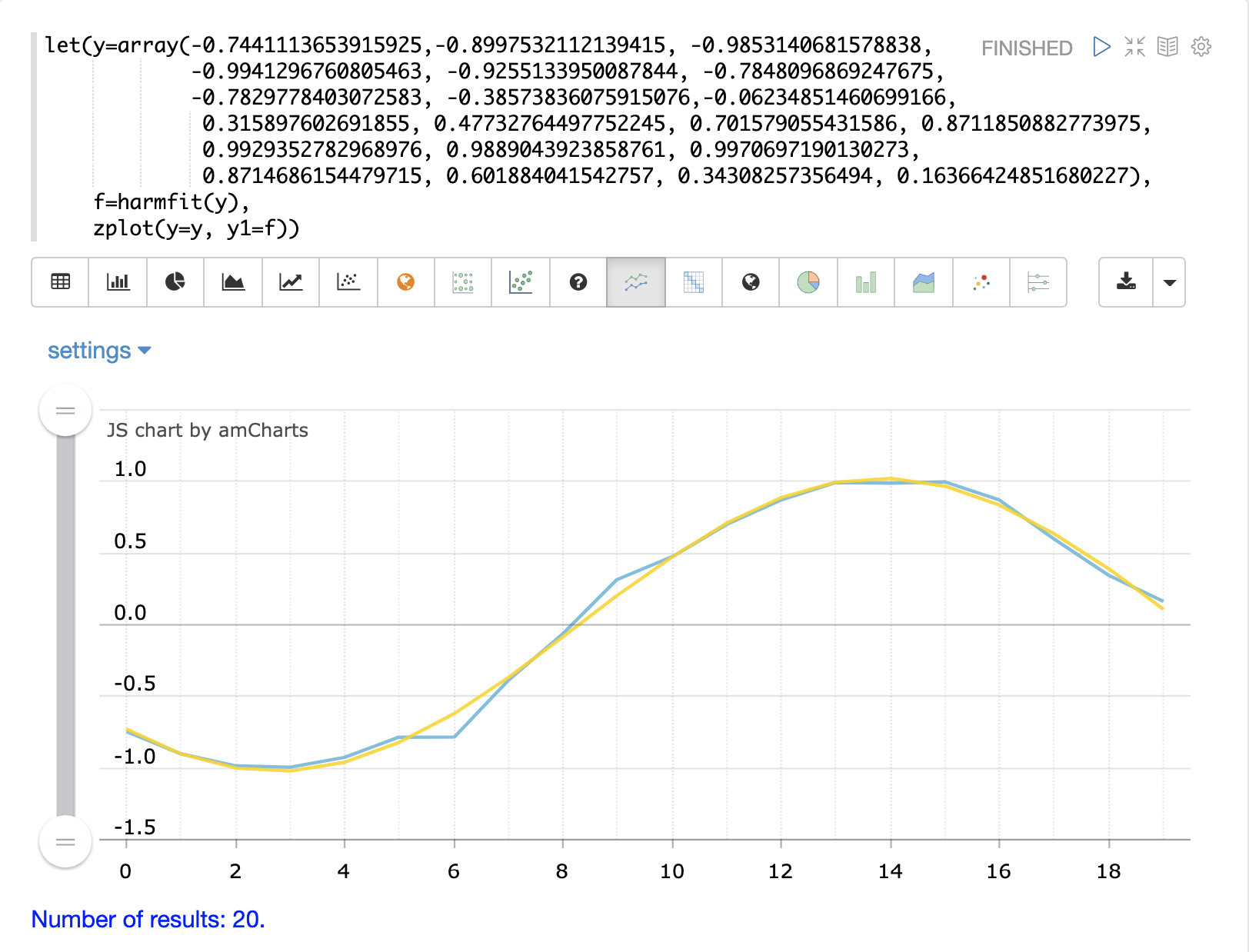
下面的示例显示了 harmfit 拟合正弦波的单个振荡。harmfit 函数返回每个控制点的平滑值。返回值也是一个模型，可由 predict、derivative 和 integrate 函数使用。

在下面的示例中，原始控制点显示为蓝色，拟合曲线显示为黄色。

harmfit 的输出是一个模型，predict 函数可以使用该模型插值和外推正弦波。在下面的示例中，natural 函数创建了一个从 0 到 127 的 x 轴，用于预测模型的结果。这将正弦波外推到 128 个点，而原始模型曲线只有 19 个控制点。