数字信号处理
本用户指南部分探讨了数字信号处理 (DSP) 领域常用的函数。
卷积
conv 函数计算两个向量的卷积。卷积的计算方式是**反转**第二个向量,并将其滑动到第一个向量上。当第二个向量滑动到第一个向量上时,计算每个点的两个向量的点积。点积收集在第三个向量中,该向量是两个向量的卷积。
移动平均函数
在查看卷积示例之前,回顾一下 movingAvg 函数很有用。移动平均函数通过在向量上滑动窗口并在每次移动时计算窗口的平均值来计算移动平均值。如果这听起来类似于卷积,那是因为 movingAvg 函数涉及类似于卷积的滑动窗口方法。
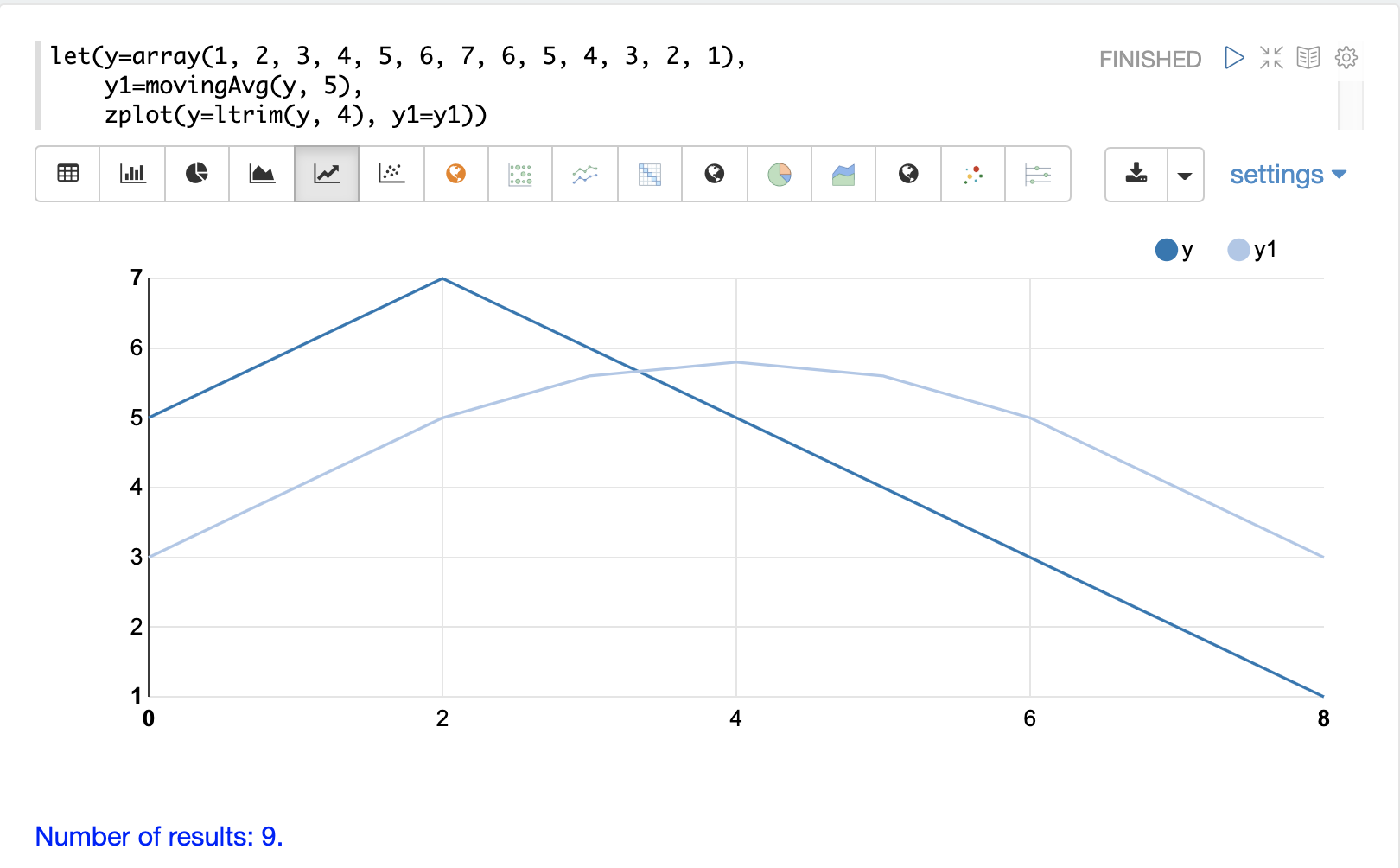
下面是一个窗口大小为 5 的移动平均示例。请注意,原始向量有 13 个元素,但移动平均的结果只有 9 个元素。这是因为 movingAvg 函数仅在具有完整窗口时才开始生成结果。ltrim 函数用于从原始 y 数组中修剪前四个元素,以与移动平均值对齐。
卷积平滑
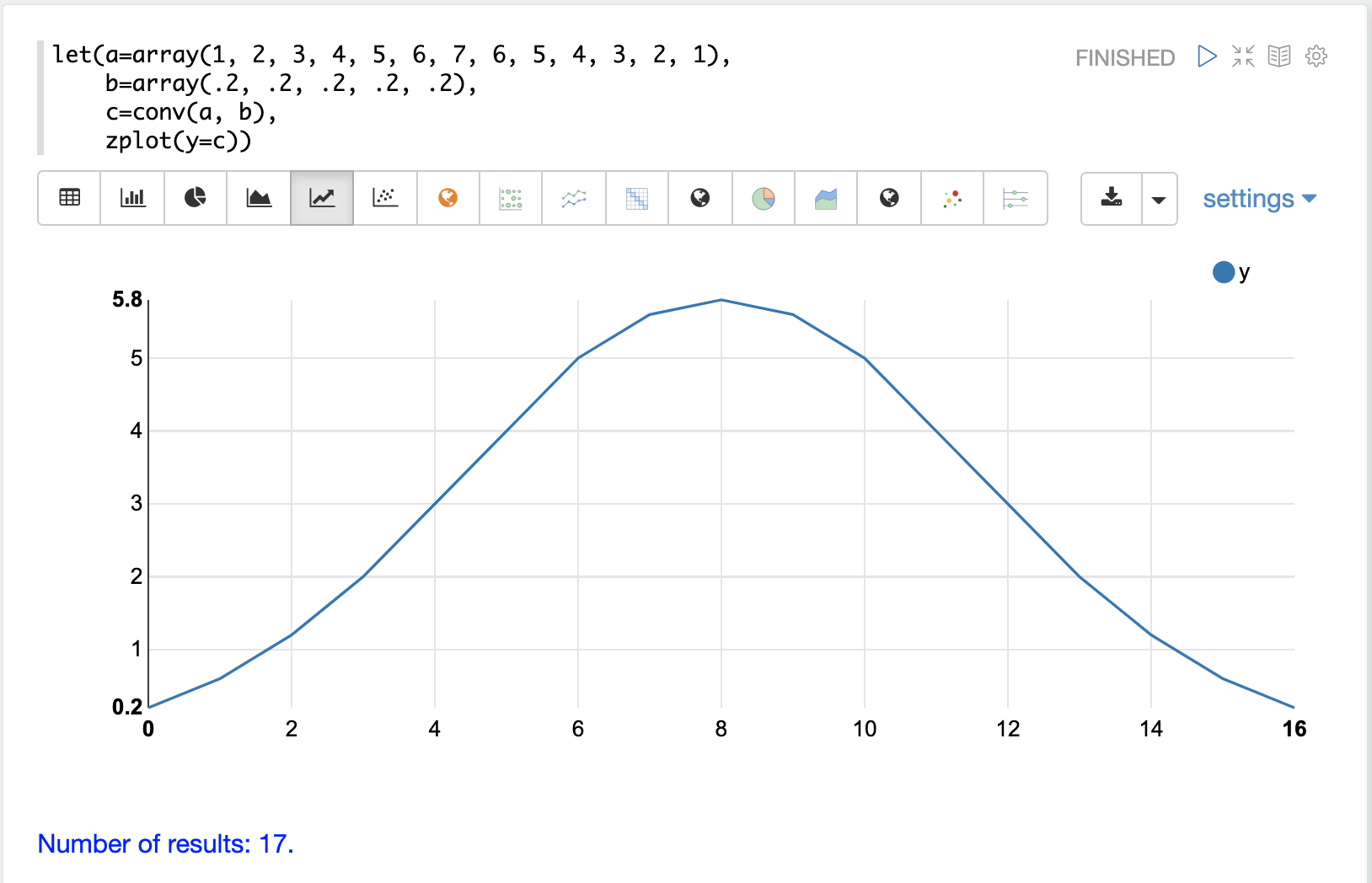
移动平均也可以使用卷积来计算。在下面的示例中,conv 函数用于通过将第二个数组应用为过滤器来计算第一个数组的移动平均值。
查看结果,我们看到卷积生成了一个包含 17 个值的数组,而不是移动平均值创建的 9 个值。这是因为 conv 函数在第一个向量的前后填充零,以便窗口大小始终完整。
我们通过使用 ltrim 和 rtrim 函数修剪卷积结果的前 4 个值和最后 4 个值来获得与 movingAvg 函数相同的结果。
下面的示例在同一图中绘制了修剪后的卷积和移动平均值。请注意,它们完美重叠。
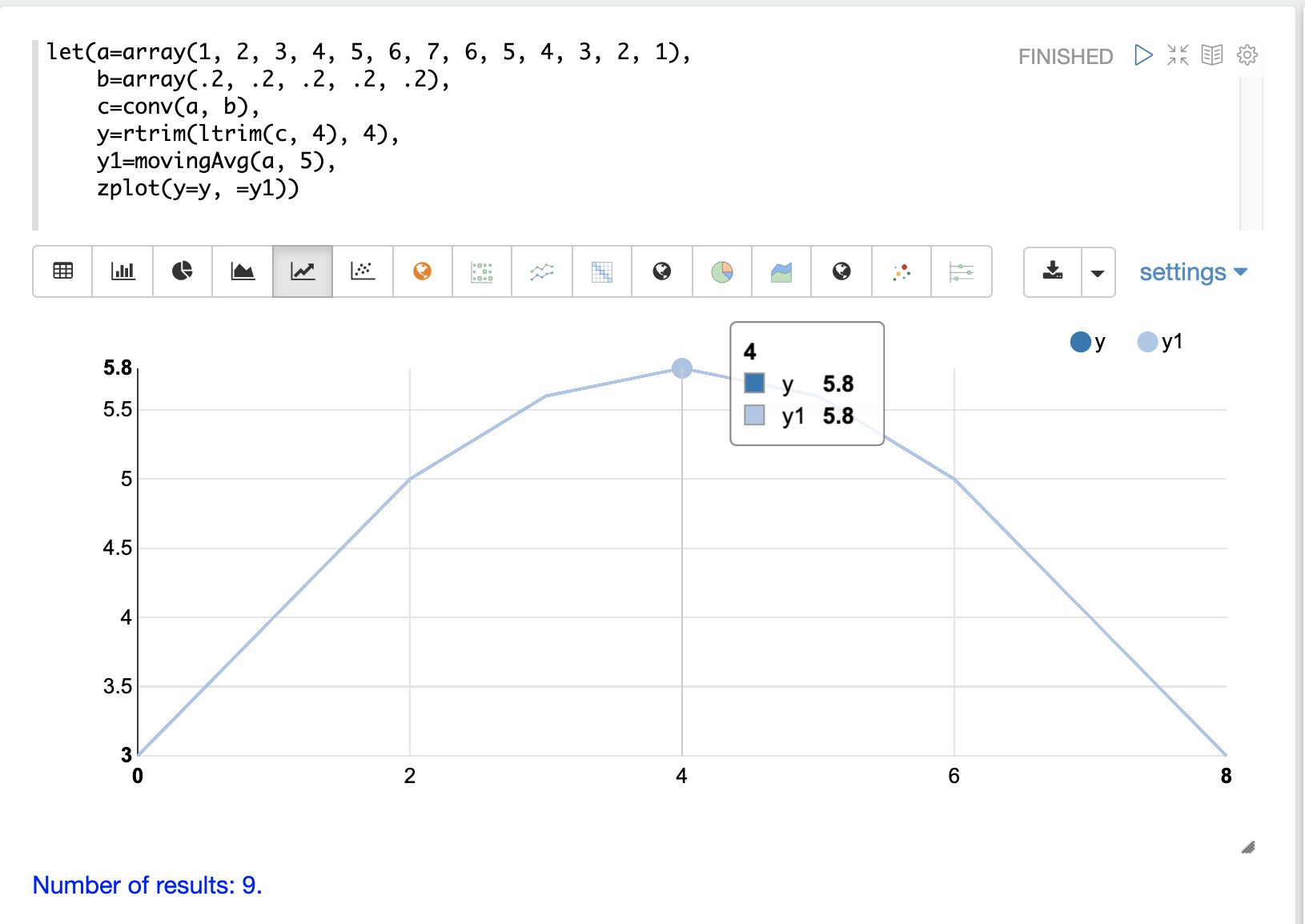
这说明了如何通过在信号上滑动滤波器并在每个点计算点积来使用卷积平滑信号。平滑效果是由滤波器的设计引起的。在示例中,滤波器长度为 5,并且滤波器中的每个值均为 .2。此滤波器使用窗口大小为 5 计算简单的移动平均值。
使用卷积计算简单移动平均值的公式是使滤波器长度为窗口大小,并使滤波器的值都相同且总和为 1。可以通过将滤波器更改为长度为 4 且每个值为 .25 来计算窗口大小为 4 的移动平均值。
更改权重
滤波器(有时称为**内核**)可以看作是权重向量。在初始示例中,滤波器中的所有值都具有相同的权重 (.2)。可以更改滤波器中的权重以产生不同的平滑效果。以下示例对此进行了演示。
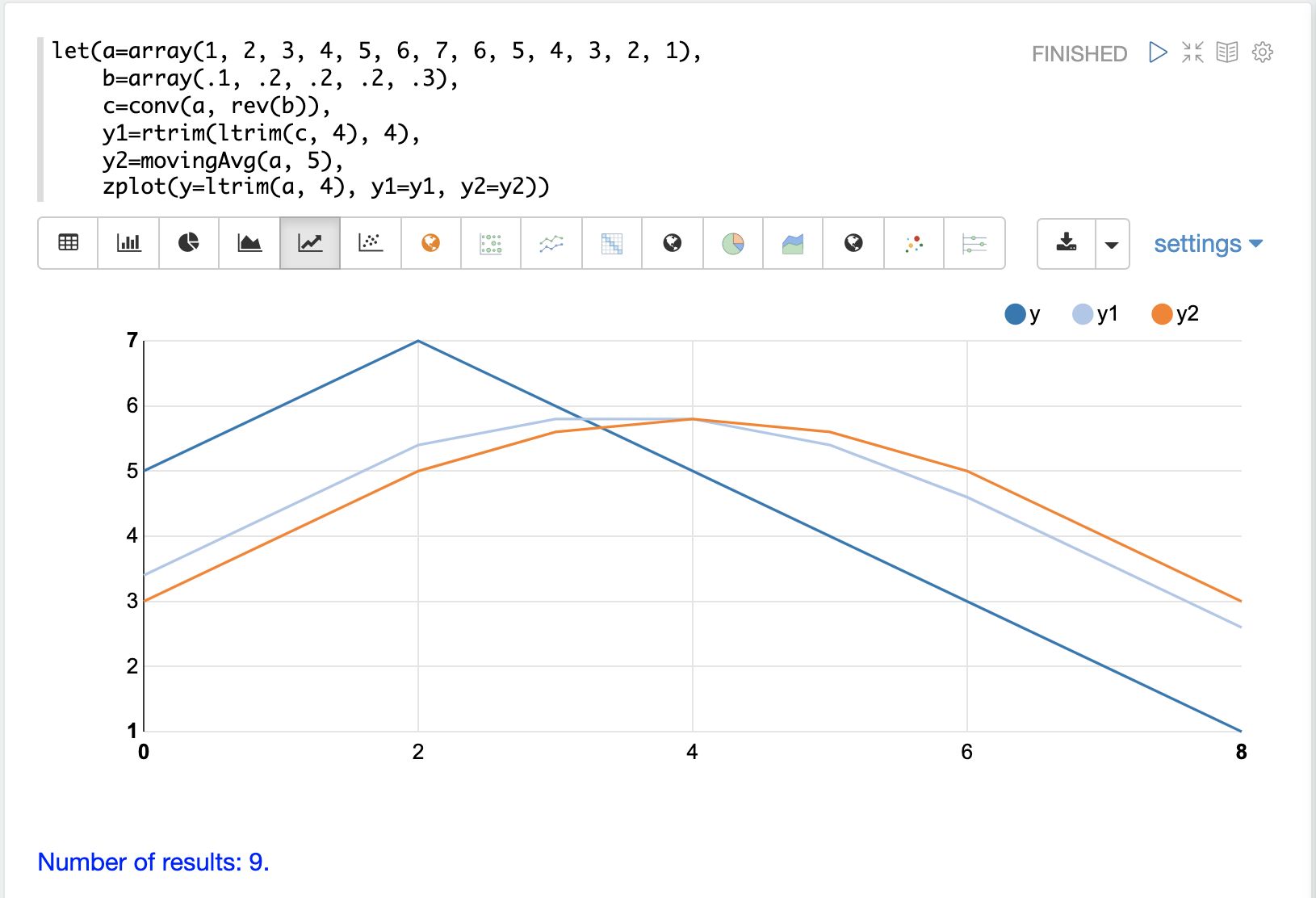
在此示例中,滤波器的权重从 .1 增加到 .3。这会将更多权重放在滤波器的前端。请注意,在 conv 函数应用之前,滤波器使用 rev 函数反转。这样做是因为卷积会反转滤波器。在这种情况下,我们提前将其反转,当卷积将其反转回来时,它与原始滤波器相同。
该图显示了滤波器中不同权重的影响。深蓝色线是初始数组。浅蓝色线是卷积,橙色线是移动平均线。请注意,卷积对底层数组中的变化响应更快。这是因为更多的权重被放在了滤波器的前端。
互相关
互相关用于确定两个信号之间的延迟。这是通过将一个信号在另一个信号上滑动,并计算每个移位处的点积来实现的。点积被收集到一个向量中,该向量表示每个移位处的关联性。互相关向量中最高的点积是两个信号最密切相关的点。
卷积中使用的滑动点积也可以用来表示两个向量之间的互相关。当表示相关性时,公式中唯一的区别是第二个向量不反转。
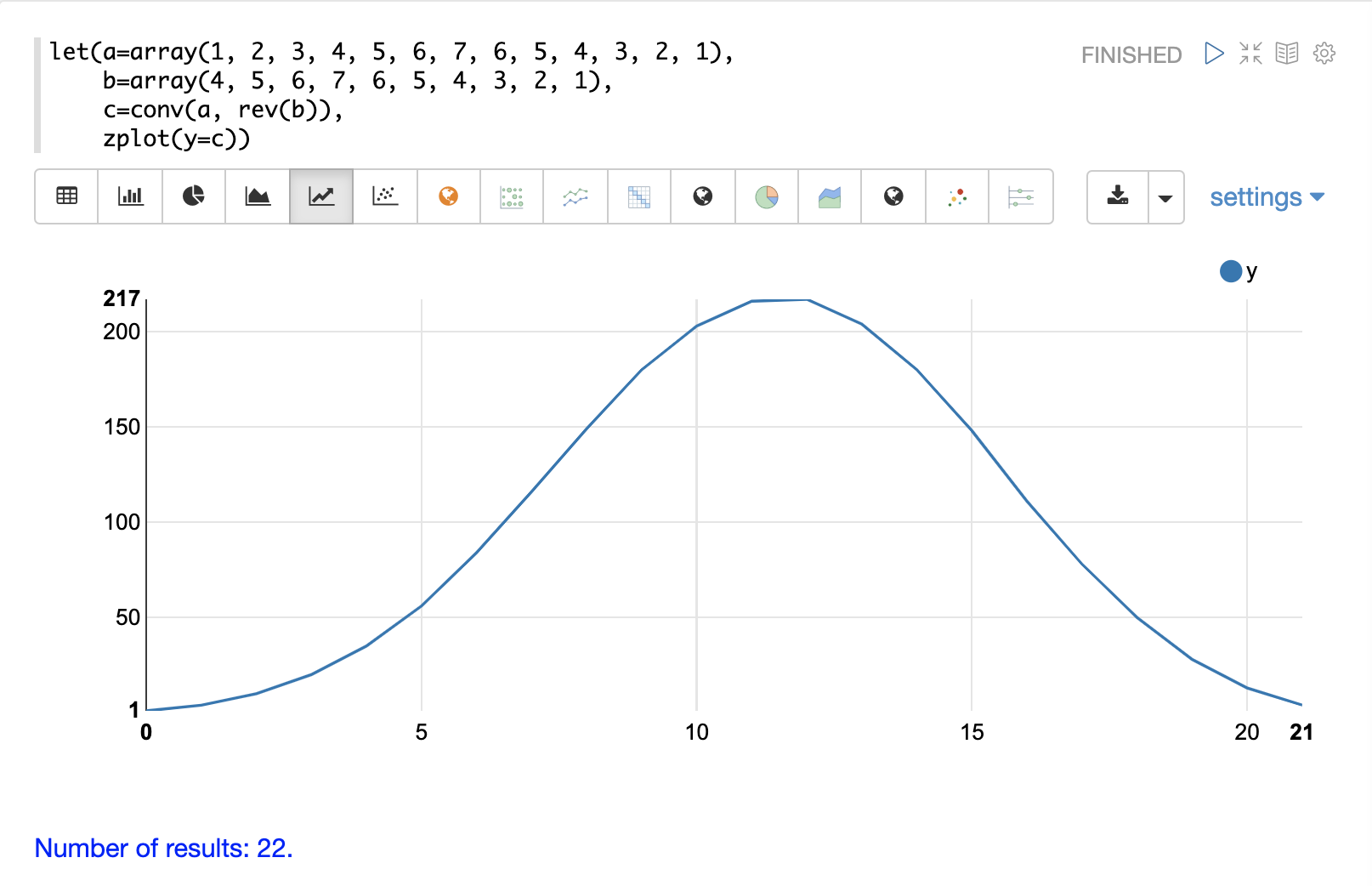
请注意,在下面的示例中,第二个向量在被conv函数操作之前,被rev函数反转。conv函数会反转第二个向量,因此它将被翻转回其原始顺序,以执行相关性计算而不是卷积计算。
请注意,在结果中,最大值为 217。这是两个向量具有最高相关性的点。
查找延迟
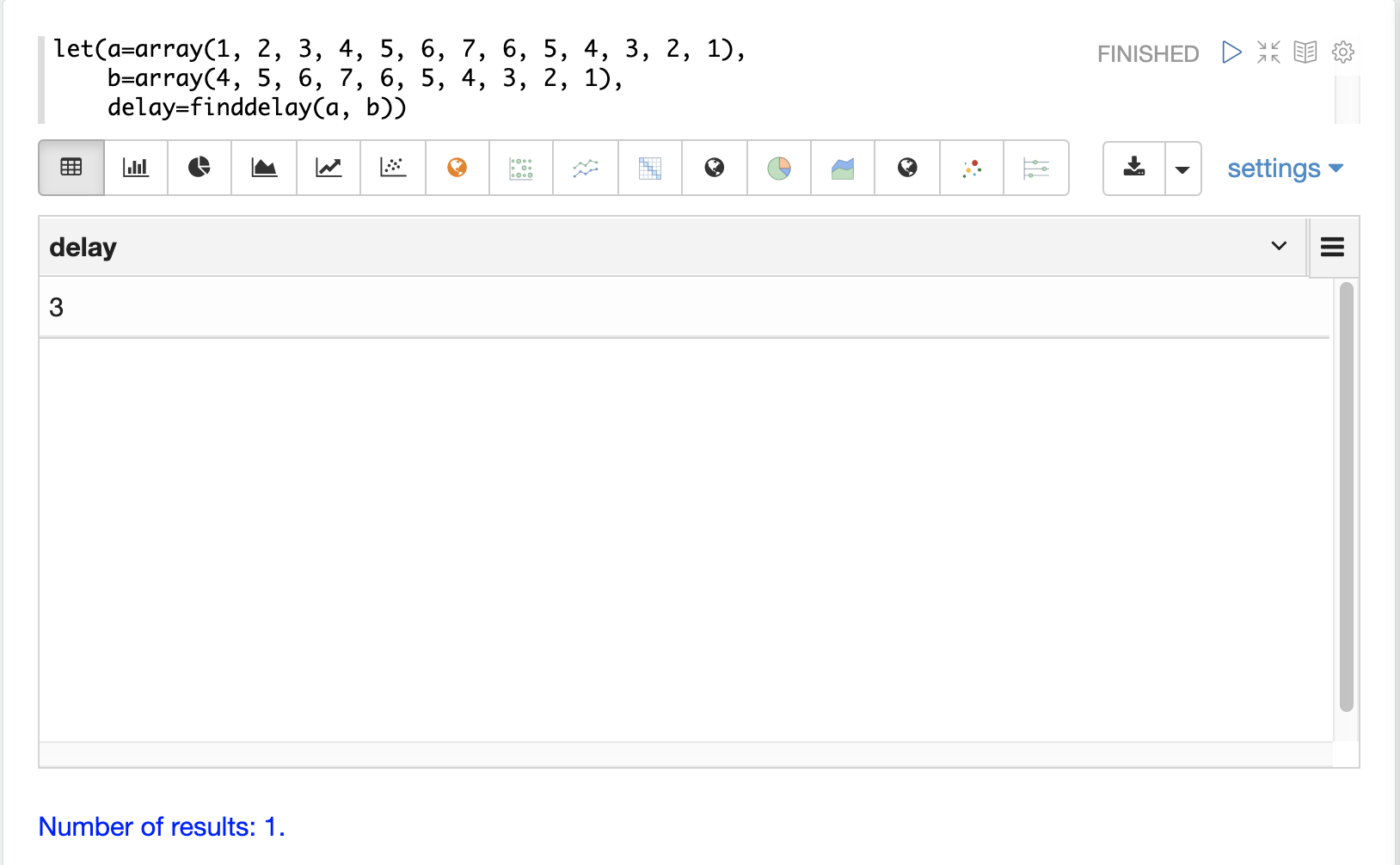
从互相关结果计算延迟相当简单,但可以使用名为finddelay的便利函数直接查找延迟。在底层,finddelay使用卷积数学来计算互相关向量,然后计算两个信号之间的延迟。
下面是finddelay函数的示例。请注意,finddelay函数报告第一个和第二个信号之间有 3 个周期的延迟。
自相关
自相关测量信号与其自身相关的程度。自相关用于确定向量是否包含信号或是纯粹随机的。
一些带有绘图的示例将有助于理解这些概念。
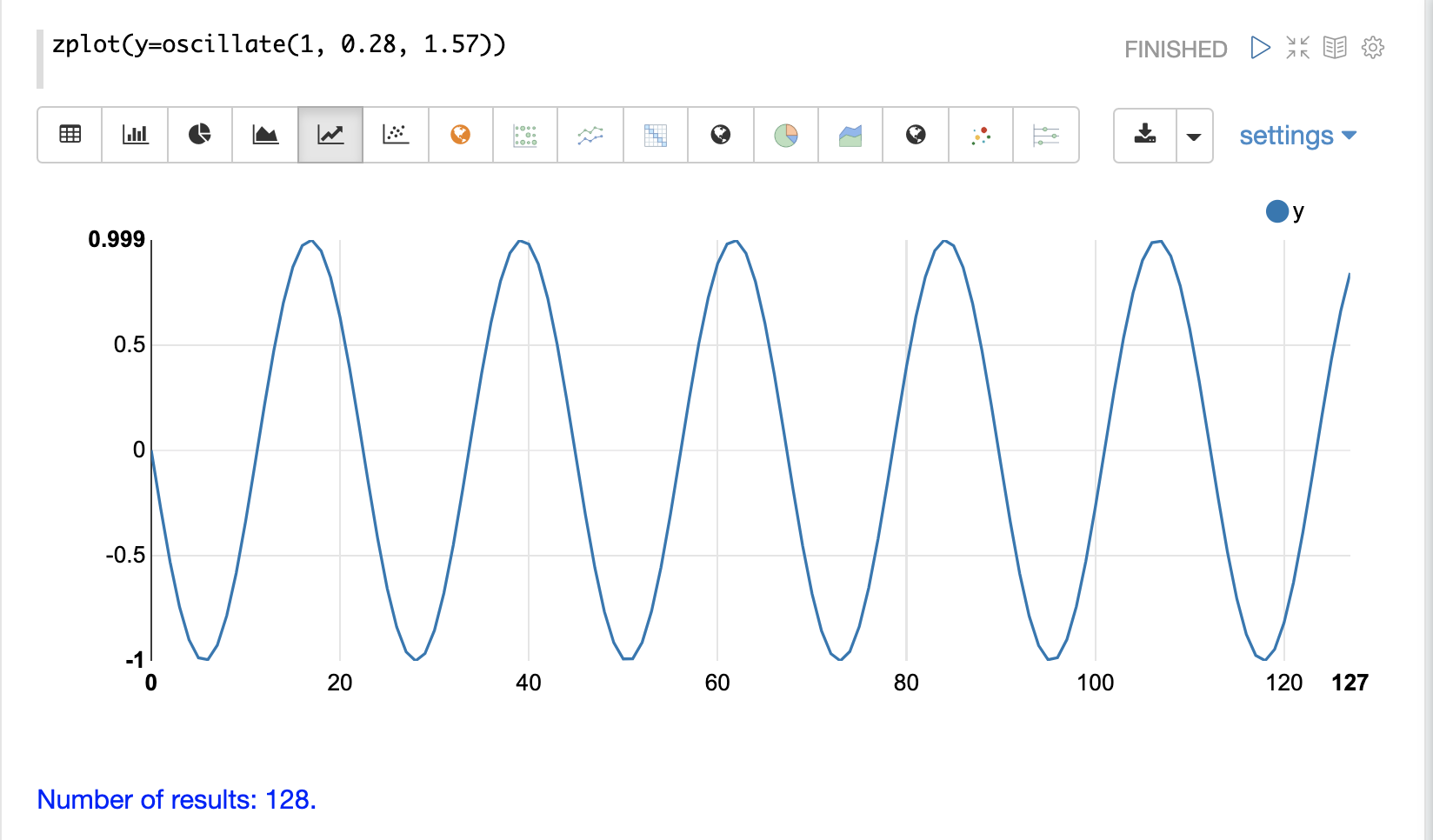
第一个示例简单地回顾了上面外推正弦波的示例。结果绘制在下面的图像中。请注意,该图有一个明显不是随机的结构。
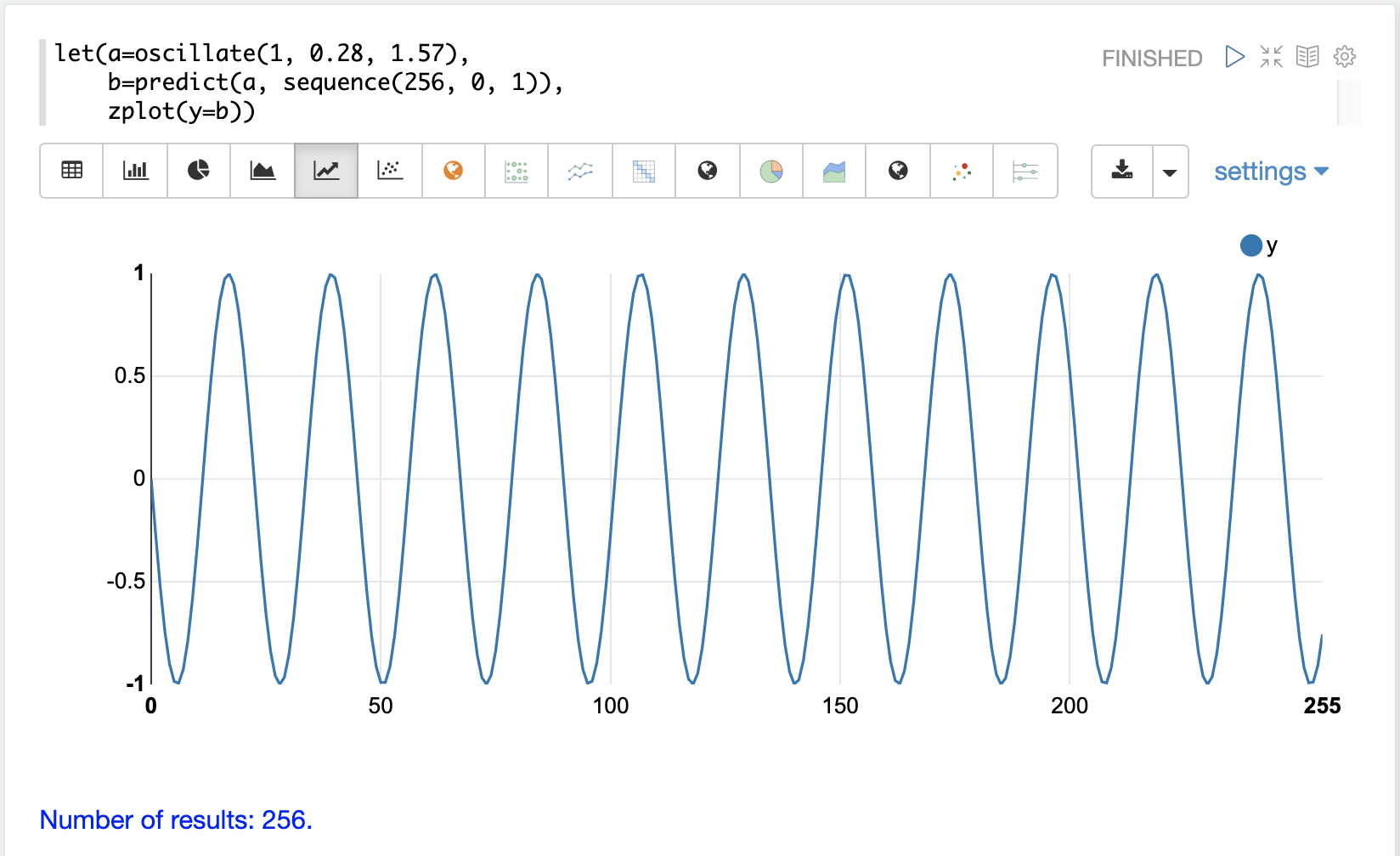
在下一个示例中,sample函数用于从uniformDistribution中抽取 256 个样本,以创建一个随机数据向量。结果绘制在下面的图像中。请注意,数据没有清晰的结构,并且数据似乎是随机的。
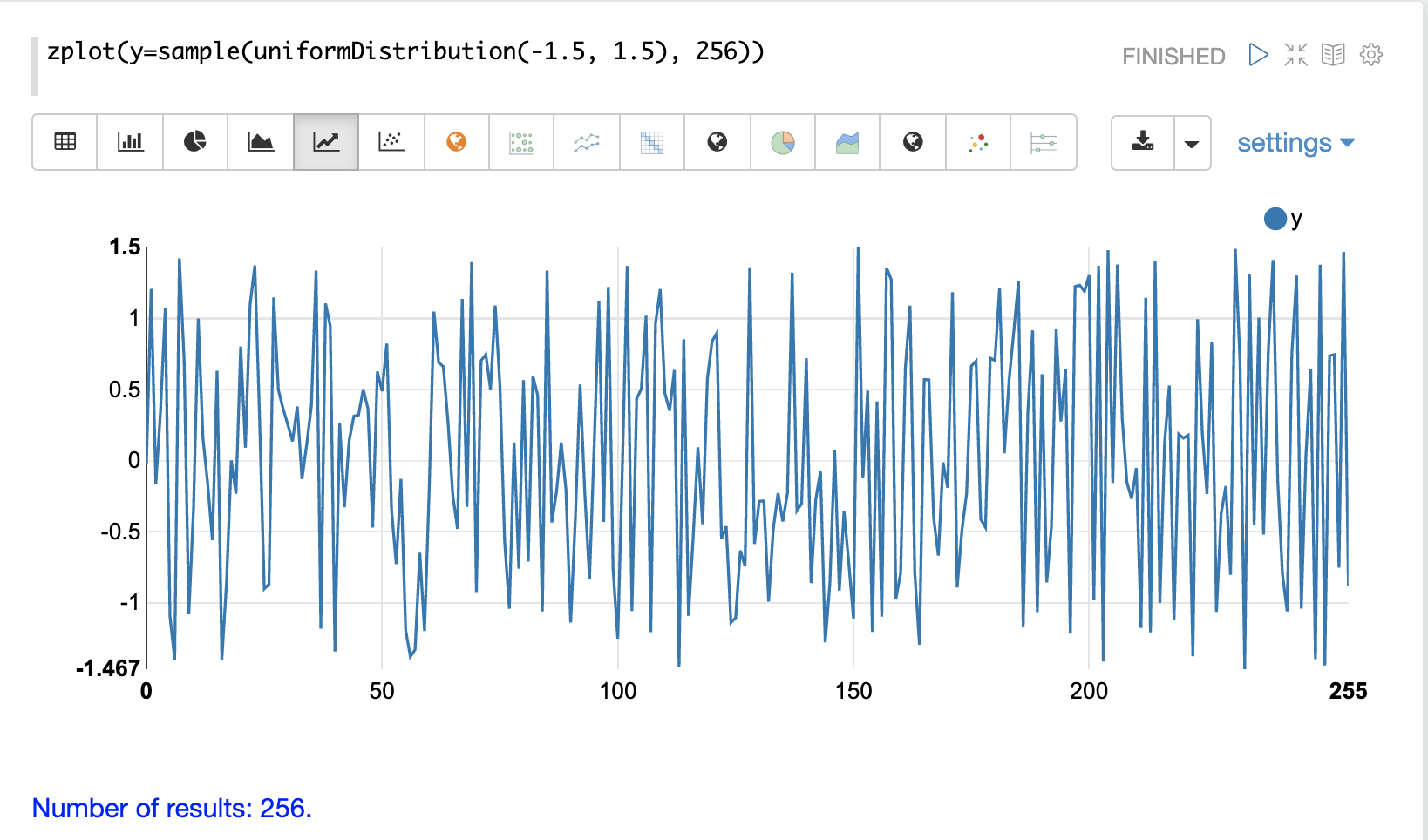
在下一个示例中,使用ebeAdd函数将随机噪声添加到正弦波中。结果绘制在下面的图像中。请注意,正弦波在一定程度上被隐藏在噪声中。很难确定是否存在结构。随着图变得越来越密集,可能很难看到隐藏在噪声中的模式。
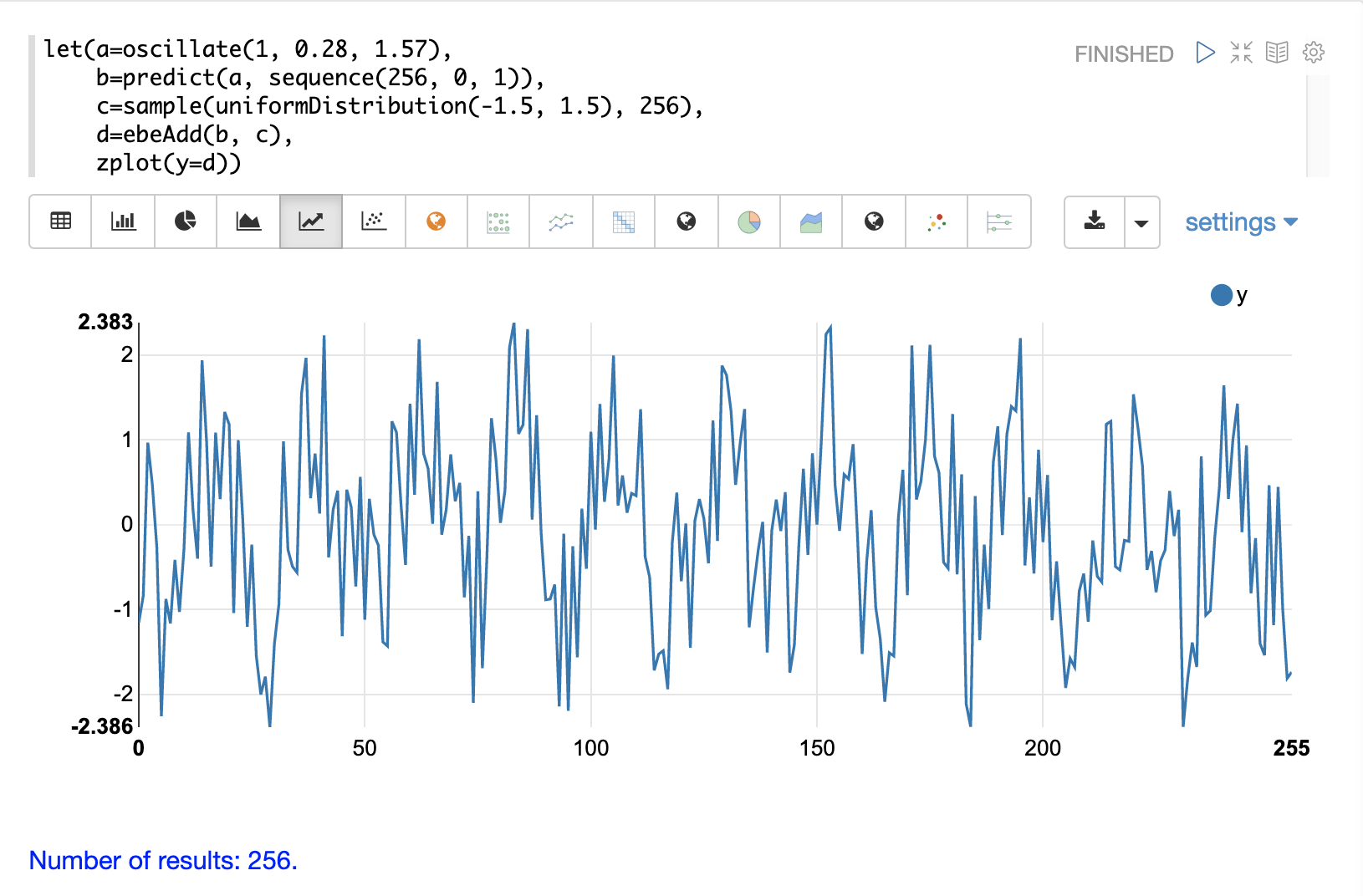
在接下来的示例中,对上面显示的每个向量执行自相关,以查看自相关图的样子。
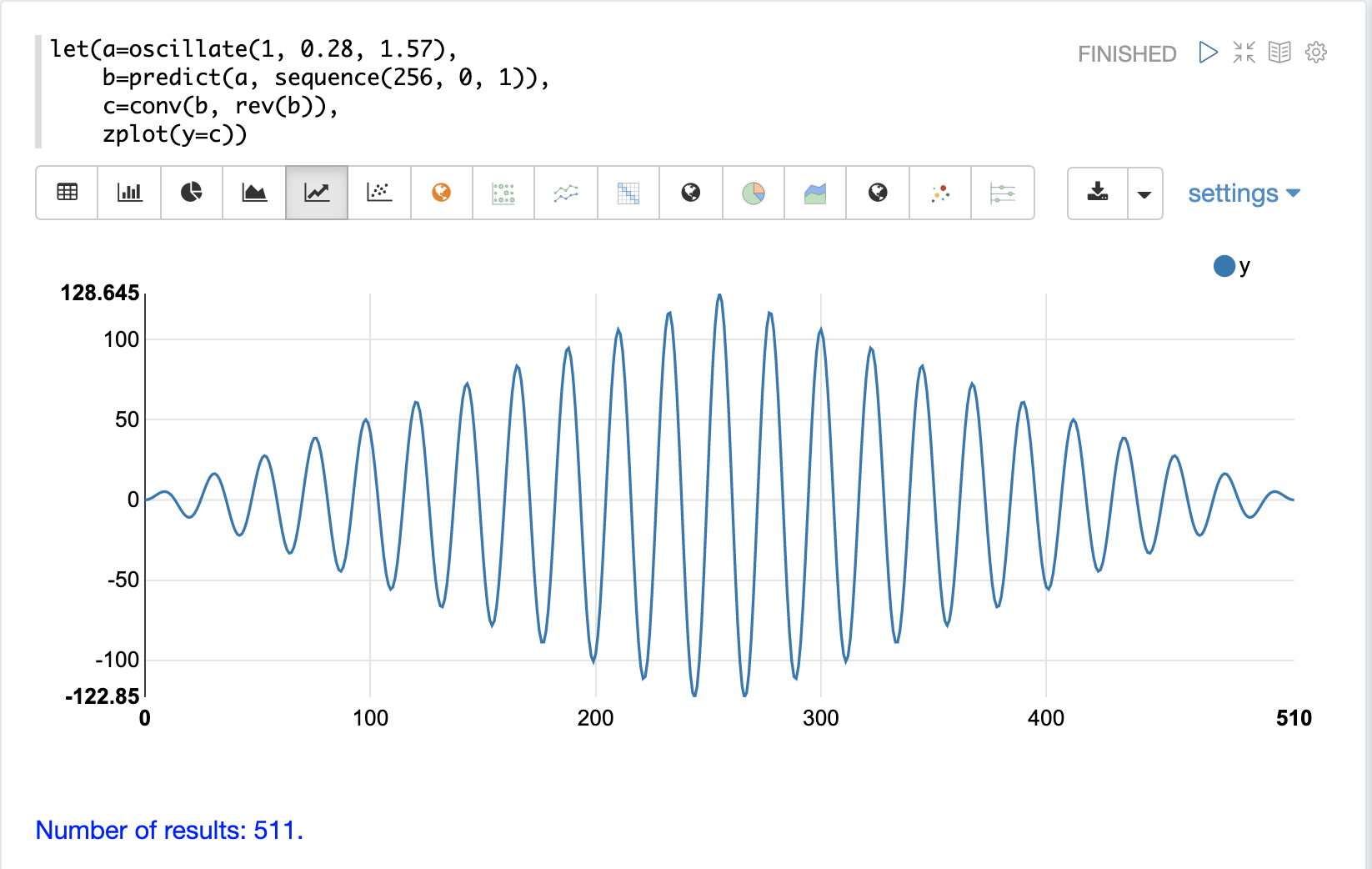
在下面的示例中,conv函数用于自相关第一个向量,即正弦波。请注意,conv函数只是将正弦波与其自身相关联。
该图具有非常独特的结构。当正弦波滑过自身的副本时,相关性会上下移动,强度会增加,直到达到峰值。此峰值直接位于中心,是正弦波直接对齐的点。在峰值之后,随着正弦波滑动得越来越远,无法直接对齐,相关性会上下移动,强度会降低。
这是纯信号的自相关图。
在下面的示例中,对纯噪声向量执行自相关。请注意,自相关图的绘图与正弦波的绘图非常不同。在此图中,存在一个长时间的低强度相关性,似乎是随机的。然后在中心,存在一个高强度相关性的峰值,其中向量直接对齐。紧随其后的是另一个长时间的低强度相关性。
这是纯噪声的自相关图。
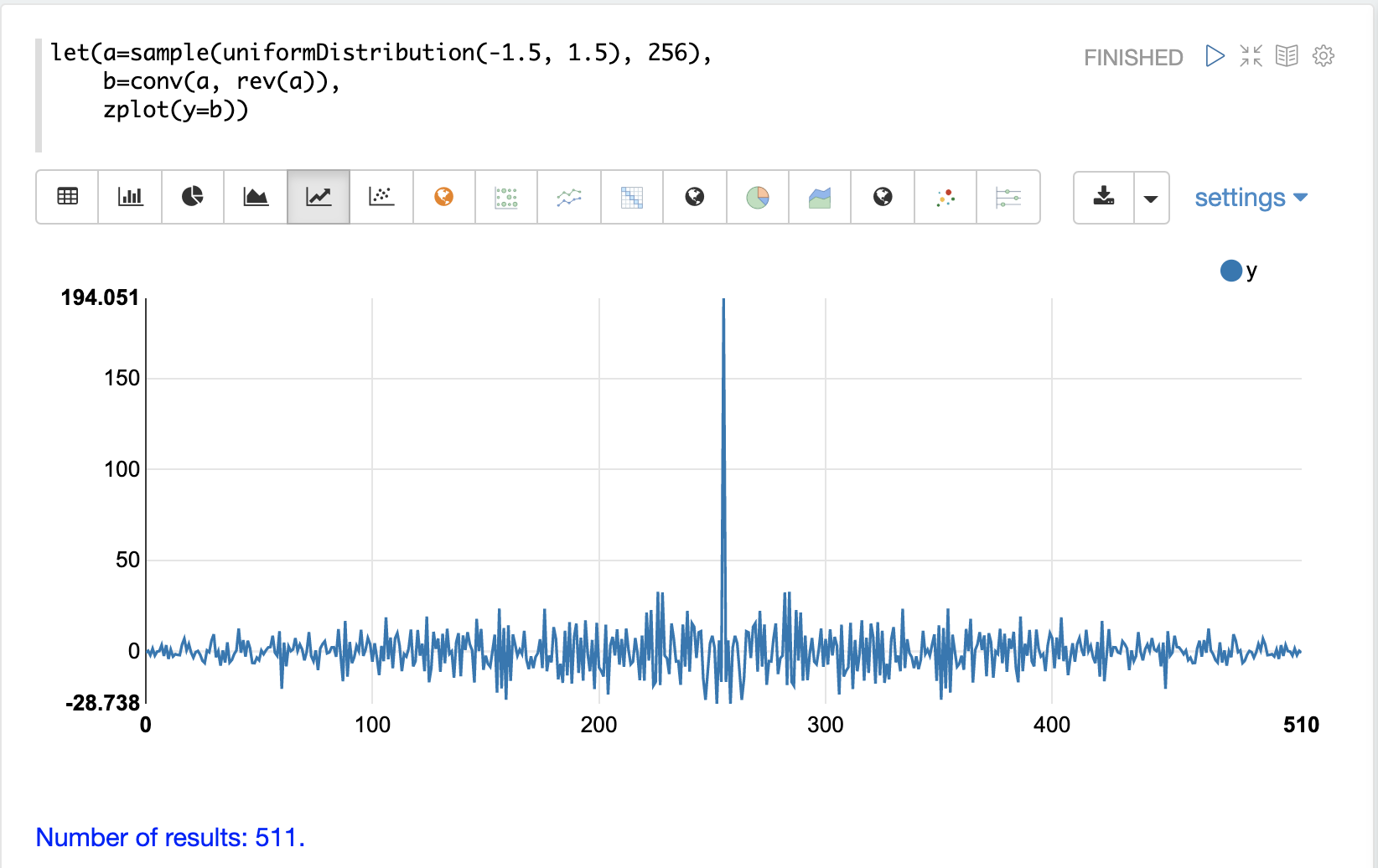
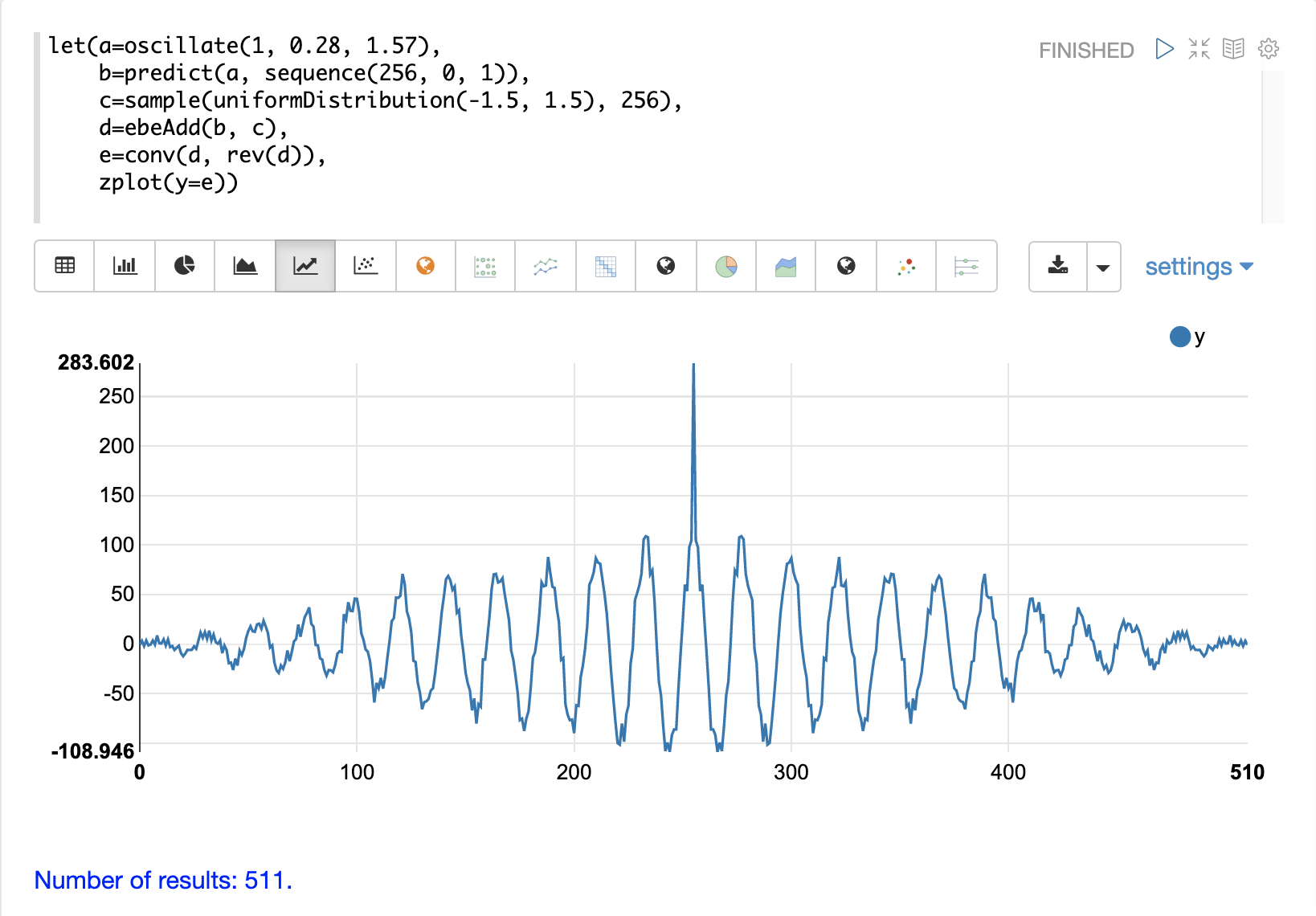
在下面的示例中,对隐藏在噪声中的正弦波向量执行自相关。请注意,此图显示出非常明显的结构迹象,这类似于纯信号的自相关图。由于噪声,相关性较弱,但相关性图的形状强烈表明存在隐藏在噪声中的基础信号。
离散傅里叶变换
上面描述的基于卷积的函数正在时域中的信号上运行。在时域中,x 轴是时间,y 轴是特定时间点某个值的数量。
离散傅里叶变换将时域信号转换为频域。在频域中,x 轴是频率,y 轴是特定频率处累积的功率。
基本原理是,每个时域信号都由一个或多个不同频率的信号(正弦波)组成。离散傅里叶变换将时域信号分解为其组成频率,并测量每个频率处的功率。
离散傅里叶变换有许多重要的用途。在下面的示例中,离散傅里叶变换用于确定信号是否具有结构或是否纯粹是随机的。
复数结果
fft函数对实数数据向量执行离散傅里叶变换。fft函数的结果以复数形式返回。一个复数有两个部分:实数和虚数。结果的实数部分描述了不同频率下信号的幅度。结果的虚数部分描述了相位。下面的示例仅处理结果的实数部分。
fft函数返回一个具有两行的matrix。矩阵的第一行是复数结果的实数部分。矩阵的第二行是复数结果的虚数部分。rowAt函数可用于访问这些行,以便将它们作为向量进行处理。
快速傅里叶变换示例
在第一个示例中,对自相关示例中使用的正弦波调用fft函数。
fft函数的结果是一个矩阵。rowAt函数用于返回矩阵的第一行,该行是一个包含fft响应的实数值的向量。
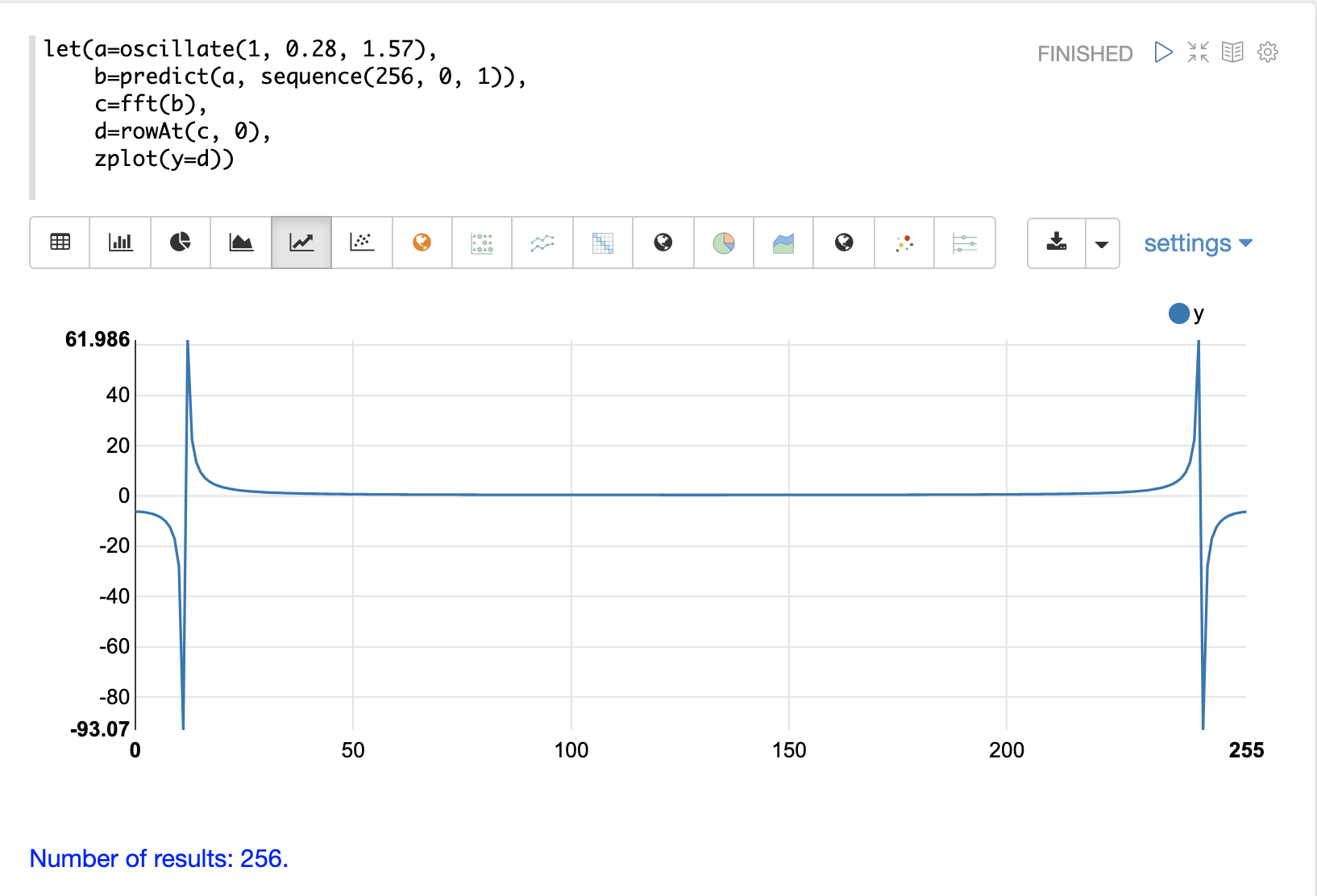
fft响应的实数值图如下所示。请注意,该图的两侧都有两个峰值。该图实际上显示的是镜像响应。该图的右侧是左侧的精确镜像。这是在对实数而不是复数数据运行fft时预期的结果。
另请注意,fft已在单个峰值中累积了大量功率。这是与正弦波特定频率相关的功率。图中绝大多数频率都具有接近 0 的功率。此fft显示了一个清晰的信号,噪声水平非常低。
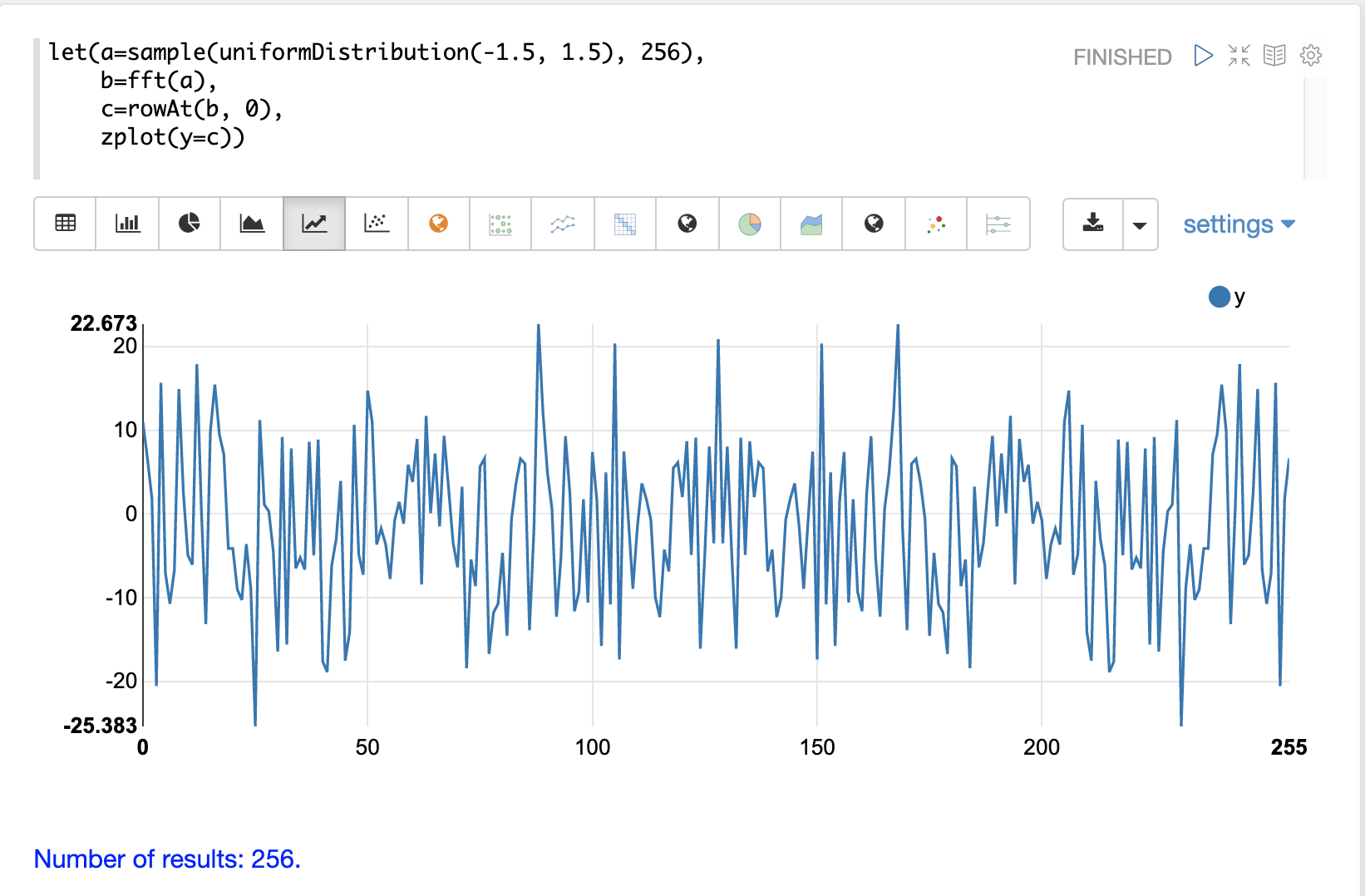
在第二个示例中,对类似于自相关示例中使用的随机数据向量调用fft函数。下面显示了fft响应实数值的图。
请注意,在此响应中没有明显的峰值。相反,所有频率都累积了随机水平的功率。此fft未显示信号的明确迹象,似乎是噪声。
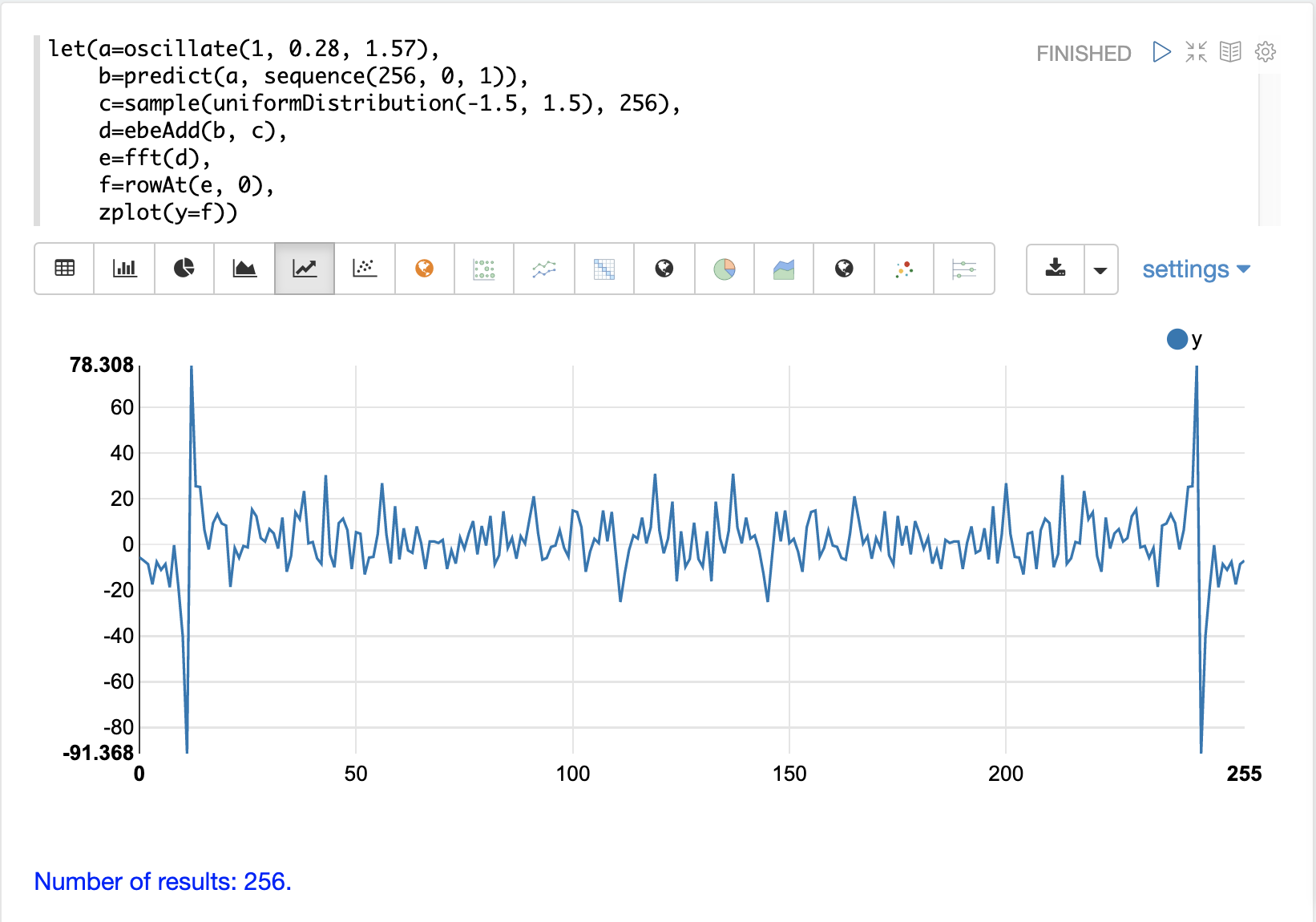
在第三个示例中,对与自相关示例中使用的隐藏在噪声中的相同信号调用fft函数。下面显示了fft响应实数值的图。
请注意,存在两个清晰的镜像峰值,其位置与纯信号的fft相同。但是,现在频率上也有相当大的噪声。fft已找到信号,并且还显示存在大量噪声以及信号。